Category: Mathematics
A dragon of genus one
I just came back from Hong Kong, where I participated in a conference on automorphic forms and all their applications. Among the talks, I especially enjoyed to hearing about the current status of the Jacquet-Langlands correspondance from Badulescu, and also the definition and properties of uniform pro--groups in the talk of Jiu-Kang Yu.
I stayed two days after the conference and had time to do some visiting and shopping. My favorite browsing time was in the Yue Hwa Chinese Emporium (the address was suggested by Yuk-Kam Lau, who also suggested the restaurant where we had our best dinner). I couldn’t resist buying the torus-shaped box that I saw there.

According to my wife, this is certainly intended to hold necklaces and bracelets. It is decorated with a dragon and what I think is a phoenix (maybe representing two elements of a basis of the homology or cohomology of the torus). I haven’t yet measured it to check if it has complex multiplication.
I took a few animal pictures, although the rather oppressive weather made it a bit difficult to spend time walking leisurely outside.



And I saw a rather melancholy piano in a side street…

Musically, I think there is a minor modernist masterpiece to be written based on the rings, whistles and noises of the Octopus card system, recorded at one of the more important exits of the MTR subway at some of its busier hours of operation.
De l’inconvénient des usines à gaz
This is maybe for the cognoscenti, but rather funny:
The Norwegian Academy of Science and Letters announces the 2017 Abel Prize is awarded to Yves Meyer, École normale supérieure Paris-Saclay, France…
(from the AMS home page, as of right now…)
I’m even prouder now than before of having bought Meyer’s “Wavelets and operators” in the Peoria, Illinois, science museum store…
MSRI introductory workshop
For the first time in my career, I am missing an event that I co-organized. Fortunately, the videos of the talks are posted on the MSRI website, and I can still profit from them…
Condorcet, Dedekind, Minkowski
One of my great pleasures in life is to walk leisurely down from my office about 30 minutes before the train (to Paris, or Göttingen, or Basel, or what you will) starts, browse a few minutes in one of the second-hand bookstores on the way, and get on the train with some wonderfully surprising book, known or not.
A few months ago, I found “Condorcet journaliste, 1790-1794”,

which one cannot call a well-known book. It is the printed version of the 1929 thesis (at the École des Hautes Études Sociales) of Hélène Delsaux, and its main goal is to survey and discuss in detail all the journal articles that Condorcet, that particularly likable character of the French revolution (about the only one to be happily married, one of the very few in favor of a Republic from the outset, and — amid much ridicule — a supporter of vote for women), wrote during those years.
Condorcet was also known at the time as a mathematician; hence this remarkable quote from the book in question:
Il est généralement admis que rien ne dessèche le coeur comme l’étude approfondie des mathématiques…
or in a rough translation
It is a truth universally acknowledged that nothing shrivels the heart more than the deep study of mathematics… [Ed. Note: what about real estate?]
This book cost me seven Francs. More recently, my trip to the bookstore was crowned by the acquisition of a reprint of R. Dedekind’s “Stetigkeit und irrationale Zahlen” and “Was sind und was sollen die Zahlen” (five Francs)

and of a first edition (Teubner Verlag, Leipzig, 1907) of Minkowski’s “Diophantische Approximationen”

for the princely sum of thirty-eight Francs.
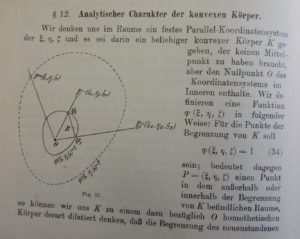
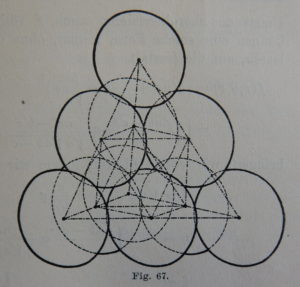
The content of Minkowski’s book is not at all what the title might suggest. There are roughly two parts, one concerned with the geometry of numbers, and the second with algebraic number theory. In both cases, the emphasis is on dimensions 2 and (indeed, especially) 3, so cubic fields are at the forefront of the discussion in the second part. This leads to a much greater number of pictures (there are 82) than a typical textbook of algebraic number theory would have today. Here are two examples,

and here is Minkowski’s description of the Minkowski functional (or gauge) of a convex set: