One of my great pleasures in life is to walk leisurely down from my office about 30 minutes before the train (to Paris, or Göttingen, or Basel, or what you will) starts, browse a few minutes in one of the second-hand bookstores on the way, and get on the train with some wonderfully surprising book, known or not.
A few months ago, I found “Condorcet journaliste, 1790-1794”,

which one cannot call a well-known book. It is the printed version of the 1929 thesis (at the École des Hautes Études Sociales) of Hélène Delsaux, and its main goal is to survey and discuss in detail all the journal articles that Condorcet, that particularly likable character of the French revolution (about the only one to be happily married, one of the very few in favor of a Republic from the outset, and — amid much ridicule — a supporter of vote for women), wrote during those years.
Condorcet was also known at the time as a mathematician; hence this remarkable quote from the book in question:
Il est généralement admis que rien ne dessèche le coeur comme l’étude approfondie des mathématiques…
or in a rough translation
It is a truth universally acknowledged that nothing shrivels the heart more than the deep study of mathematics… [Ed. Note: what about real estate?]
This book cost me seven Francs. More recently, my trip to the bookstore was crowned by the acquisition of a reprint of R. Dedekind’s “Stetigkeit und irrationale Zahlen” and “Was sind und was sollen die Zahlen” (five Francs)

and of a first edition (Teubner Verlag, Leipzig, 1907) of Minkowski’s “Diophantische Approximationen”

for the princely sum of thirty-eight Francs.
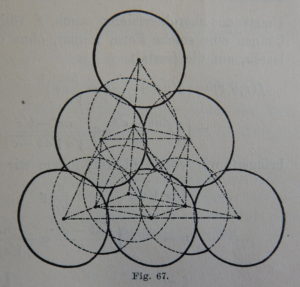
The content of Minkowski’s book is not at all what the title might suggest. There are roughly two parts, one concerned with the geometry of numbers, and the second with algebraic number theory. In both cases, the emphasis is on dimensions 2 and (indeed, especially) 3, so cubic fields are at the forefront of the discussion in the second part. This leads to a much greater number of pictures (there are 82) than a typical textbook of algebraic number theory would have today. Here are two examples,

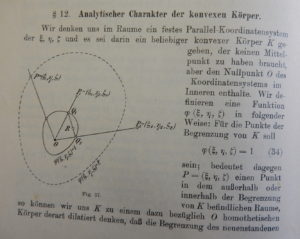
and here is Minkowski’s description of the Minkowski functional (or gauge) of a convex set: