Page 31 – E. Kowalski's blog

And then there was one in 744

The feared grains of salt have reared their ugly heads: the growth exponent 1/186 that I mentioned in my last post has been reduced to 1/744. I had missed the fact that, in order to avoid dealing with elements of trace 0, I first had to replace the generating set $H$ with $H\cdot H$ , alas… But the previous exponent does work for any generating set which contains a regular semisimple element with non-zero trace.

[P.S. For the Lubotzky group, the spectral gap goes down to something like $2^{-2^{36}}$ …]

Explicit growth for generating subsets of SL_2 over finite fields

I have one more lecture next week in my expander class, but today I finished the proof of Helfgott’s growth theorem for $\mathrm{SL}_2(\mathbf{F}_p)$ . As I had hoped, I did this in my notes with explicit constants (I didn’t try to follow those constants on the blackboard).

Taking into account some grains de sel, since there may well be minor computational mistakes lurking around (though I have already corrected a few), the result I obtain is the following: if $p\geq 7$ is prime, and if $H\subset \mathrm{SL}_2(\mathbf{F}_p)$ is a symmetric generating set, containing $1$ for simplicity, then either the triple product
$H^{(3)}=\{xyz\,\mid\, x,y,z\in H\}$
is all of $\mathrm{SL}_2(\mathbf{F}_p)$ , or otherwise we have
$|H^{(3)}|\geq \frac{1}{2}|H|^{1+\delta}$
where
$\delta=\frac{1}{186}=0.0053763440860215053763440860215053763441\ldots$

(Of course, the factor $1/2$ can be incorporated into a slightly-smaller exponent, but that introduces an ugly-looking dependency on the size of $H$ , which one must recover using an uglier trivial bound for $|H|$ small, so I preferred this version…)

The current version of the notes contains the argument, though it is a bit rough (I will soon rearrange some of it, to attempt to provide more motivation — at least the way I understand how it goes…)

For the proof, I followed the clear outline in the first sections of the paper of Pyber and Szabó. This reduces the problem, rather quickly and cleanly, to a “non-concentration” estimate for the intersection of $H$ with a regular-semisimple conjugacy class $C$ , of the type
$|C\cap H|\leq c|H^{(k)}|^{2/3}$
for some fixed $k$ and absolute constant $c$ . This inequality is now commonly called a (generalized) Larsen-Pink inequality (the prototype going back to the late 90’s preprint — now published — of Larsen and Pink for the non-concentration of finite subgroups of algebraic groups in subvarieties). Though the general case is quite tricky, there is here an easy enough argument, based on studying the fibers of the map
$(x_1,x_2,x_3)\mapsto (x_1x_2,x_1x_3)$
where the three arguments $x_i$ are all in $C$ (this is the basic idea already presented by Larsen and Pink to explain their result, in another case).

It turns out that, if one imposes that $C$ is not the conjugacy class of elements of trace 0, which can be ensured (using bare hands) by “escape from subvarieties”, the cases where this map has positive-dimensional fibers are rather simple to analyze (I owe this computation to R. Pink…)

Moreover, only one case requires another instance of Larsen-Pink-type inequalities (those readers who have looked at the paper of Larsen and Pink, or the one of Breuillard-Green-Tao which has a general “approximate” version, will know that there is a rather complicated induction involved in general), and it is a very easy one: if $U$ is the subgroup of upper-triangular unipotent matrices, then
$|U\cap H|\leq 1+|H^{(5)}|^{1/3}\leq 2|H^{(5)}|^{1/3},$
which is an instructive exercise. (In fact, in rearranging this section of my notes, I will use this as a motivating example…)

With this final ingredient, I can now produce (with the same amount of salt…) an effective spectral gap for the Cayley graphs of the Lubotzky subgroup of $\mathrm{SL}_2(\mathbf{Z})$ , generated by
$u=\begin{pmatrix} 1& 3\\ 0&1\end{pmatrix},\quad\quad v=\begin{pmatrix} 1&0\\3&1\end{pmatrix},$
modulo primes, namely (drumroll) for $p$ large enough (drumroll; but I won’t tell you how large today), we have (drumroll)
$\lambda_1(\Gamma_p)\geq 2^{-2^{34}}.$

(Actually, I already know various points of inefficiency in my treatment of the Bourgain-Gamburd expansion argument which should lead to some improvements, and I hope to find other avenues to explore and stones to turn to do better…)

What is the Cayley graph of the cyclic group of order 2?

Here is an amusing thing I hadn’t properly realized until recently: depending on the definition, the Cayley graph of $\mathbf{Z}/2\mathbf{Z}$ with respect to the symmetric generating set $\{1\}$ can be either a single arrow joining two vertices

or a cycle of length 2:

The first case occurs when one is not careful, taking as edge set of $\mathcal{C}(G,S)$ the set
$E=\{\{g,gs\}\,\mid\, g\in G\,\ s\in S\}$
(as was probably to be expected, my notes on expander graphs use this naïve definition…)

The second case occurs (at least) when one is Serre, as can be checked from the definition in “Trees”, and the resulting illustration:

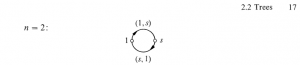
(in a French printing of that book which I have seen, Serre specifically warns that the two edges are not the same).

The questions are, which is the “right” definition, if any? and should this matter? To a large extent, the answer to the second is (fortunately) “not really”, though the same issue arises for any Cayley graph where some generator is an involution.

Either choice has some potentially annoying features:

(1) The canonical choice (Serre’s) has the effect that any Cayley graph of a group with respect to a generating set containing an involution has multiple edges; for instance, the following picture taken from P. de la Harpe’s “Topics in geometric group theory”

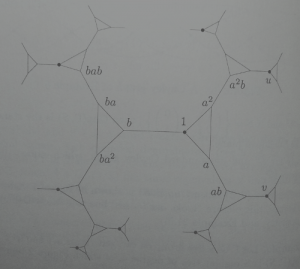
is supposed to be the Cayley graph of $\mathrm{PSL}_2(\mathbf{Z})$ with respect to a generating set for which it is a free product of cyclic groups of order 2 and 3 (generated by $b$ and $a$ , respectively), but is wrong with the canonical definition. (To be fair, de la Harpe mentions the issue, and says that he uses the naïve definition because that is not a problem for his purposes.)

(2) In the canonical choice, the formula
$M\varphi(x)=\frac{1}{|S|}\sum_{s\in S}{\varphi(xs)}$
for the Markov averaging operator is usually wrong. (E.g., for the example of $\mathrm{PSL}_2(\mathbf{Z})$ above.) In particular, the spectrum of the Laplace operator is not the same depending on which definition is used…

(3) Similarly, the Cayley graph $\mathcal{C}(G,S)$ is not always $|S|$ -regular.

(4) However, in the non-canonical choice, it follows that a Cayley graph of a finite group may have infinite girth (being a tree, as in the example of $\mathbf{Z}/2\mathbf{Z}$ …) Correspondingly, the interpretation of the girth of a Cayley graph as the smallest length of a non-trivial relation in the generators may fail…

At the moment, as I said, I use the naïve definition in my notes (most books I’ve seen which bother to define the Cayley graph in a formally precise way seem to do the same, though the definition is often sufficiently fuzzy that it doesn’t take much effort to accommodate both possibilities…) But I claim somewhere that the Cayley graph of $\mathbf{Z}/m\mathbf{Z}$ (with respect to $\{\pm 1\}$ ) is a cycle of length $m$ , which is then wrong for $m=2$ .

I haven’t quite decided how I will change the text, since I tend to like the formula for the Markov averaging operator. Maybe, like de la Harpe, I will just mention both possibilities and use the naïve one. Certainly, as far as expander graphs are concerned, this has no consequence on the property of being or not an expander for a sequence of Cayley graphs (of bounded valency).

Explicit multiplicative combinatorics

One of the goals of my course on expanders is to (try to) get an explicit spectral gap for the Cayley graphs of $\mathrm{SL}_2(\mathbf{F}_p)$ , for $p$ prime, with respect to the generating set
$S_p=\{u,u^{-1}, v,v^{-1}\}$
where
$u=\begin{pmatrix} 1& 3\\ 0&1\end{pmatrix},\quad\quad v=\begin{pmatrix} 1&0\\3&1\end{pmatrix}$
(which corresponds to the reduction modulo $p$ of the Cayley graph of the “Lubotzky group” $L$ , generated in $\mathrm{SL}_2(\mathbf{Z})$ by the “same” matrices.)

The first thing to do in order to obtain an explicit estimate is to get an explicit form of the relation between “pairs of sets with large multiplicative energy” and “cosets of a common approximate group” — indeed, this is a crucial point in the first step of the argument discovered by Bourgain and Gamburd to derive expansion for some Cayley graphs from a classification of approximate subgroups (or more directly, of sets with “small tripling”, a classification which had been produced by Helfgott for $\mathrm{SL}_2(\mathbf{F}_p)$ ).

To explain this, recall that if $A, B\subset G$ are subsets of a finite group $G$ , the normalized multiplicative energy $e(A,B)$ is defined by
$e(A,B)=|\{(x_1,y_1,x_2,y_2)\in A^2\times B^2\,\mid\, x_1y_1=x_2y_2\}|/(|A||B|)^{3/2}.$
It is easy to show that $e(A,B)\leq 1$ , and it is a pleasant exercise to prove that the extreme case $e(A,B)=1$ occurs if and only if there exists a subgroup $H$ of $G$ and elements $x$ , $y$ of $G$ such that
$A=xH,\quad\quad B=Hy.$

The Bourgain-Gamburd argument depends on understanding sets $A$ and $B$ such that
$e(A,B)\geq |G|^{-\varepsilon}$
for some (small) $\varepsilon>0$ .
This can now be done, in some cases, by first proving an “approximate” version of the characterization of the extreme $e(A,B)=1$ , and then classifying the resulting “approximate” objects. The second step is much more involved, and I won’t talk about it here, but the first can be done in full generality. The standard texts explaining this are the book of Tao and Vu and a paper of Tao (which contains more details than the summary in the book.)

It is clear from reading the proofs that they are “effective”, but these sources do not give explicit inequalities. So I did the exercise of going through the arguments to get actual constants, inputing the recent explicit results of Petridis to get better control on product sets than the corresponding argument in Tao’s paper. After three or four rounds of checks, I get the following: if
$e(A,B)\geq \frac{1}{\alpha},$
then there exist a $\beta$ -approximate subgroup $H$ of $G$ and elements $x$ , $y\in G$ ,
such that
$|H|\leq \beta_2|A|,\quad\quad |A\cap xH|\geq \beta_1^{-1}|A|,\quad\quad |B\cap Hy|\geq \beta_1^{-1}|B|,$
where
$\beta\leq 2^{14257}\alpha^{6330},\quad\quad \beta_1\leq 2^{14667}\alpha^{6553},\quad\quad \beta_2\leq 2^{283}\alpha^{126},$
(and a $\beta$ -approximate subgroup is defined to be a symmetric subset, containing the identity, such that $H\cdot H\subset X\cdot H$ for some subset of size $|X|\leq \beta$ .)

For the moment, I’ve only typed a very condensed note spelling this out, which is found on my page of unpublished notes; I admit that I had some fun devising an arrow notation to simplify keeping track of the relation and sizes between the sets involved…

All this will be incorporated in my lectures notes on expanders, and then expanded later to a full proof so that the latter are self-contained. I will also attempt to improve these constants, which are not very promising when I think of what the spectral gap will become in the end…

Parentheses

I have a weakness for programming languages. Given the time and opportunity, I would gladly learn a new one every few months, and apart from TeX (in its programming language guise) and Perl, which I both abhor because of their atrocious syntax, I usually find something to like in all languages. I have even composed what may be the only illustrated children story ever written in pure Postscript (“The story of the triangle that grew”.) But my favorite language remains Lisp, especially in its Common Lisp variant, which is the one I know best (with Emacs Lisp a close second). I was therefore saddened to learn today of that the creator of Lisp, John McCarthy, recently passed away.

(Interestingly, according to Wikipedia, McCarthy had a PhD in math under Lefschetz…)