Will Sawin and I just put up on arXiv a preprint that is the natural follow-up to our paper on those most alluring of shapes, the Kloosterman paths.
As the title indicates, we are looking this time at the support of the limiting random Fourier series that arose in that first paper, namely
where is a sequence of independent Sato-Tate-distributed random variables. In a strict sense, this should be a very short paper, since the computation of the support is easily achieved using some basic probability and elementary properties of Fourier series: it is the set of continuous functions
such that (1) the value of
at
is real and belongs to
; (2) the function
has purely imaginary Fourier coefficients
for
; (3) we have
for all
.
So why is the paper 26 pages long? The reason is that this support (call it ) is a rather interesting set of functions, and we spend the rest of the paper exploring some of its properties. Most importantly, the support is not all functions, so we can play the game of picking our favorite continuous function on
(say
) and ask whether or not
belongs to
.
For instance:
- Fixing a prime
, and
,
invertible modulo
, does the Kloosterman path
itself belong to the support? Simple computations show that it depends on
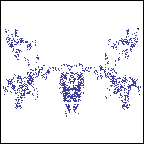
! For instance, the path for the Kloosterman sum
, shown below, does not belong to the support. (As we observe, it looks like a Shadok, whose mathematical abilities are well-known — sorry, the last link is only in French ; I suggest to every French-aware reader to watch the corresponding episode, since the voice of C. Piéplu achieves the seemingly impossible in making this hilarious text even funnier…)
Kl_2(8,1;19) - On the other hand, the path giving the graph of the Takagi function
(namely
) belongs to the support.
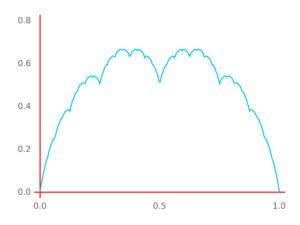
Takagi function -
But maybe the most interesting problem from a mathematical point of view is one of pure analysis: when we see a Kloosterman path (such as the one above), we only see its image as a function from
to
, independently of the parameterization of the path. So we can take any shape in the plane that can be represented as the image of a function
satisfying the conditions (1) and (2) above, and ask: is there a reparameterization of
that belongs to the suppport? For instance, for the Kloosterman paths themselves (as in (1) above), it is not difficult to find one: instead of following each of the
segments making the Kloosterman path in time
, one can insert a “pause” of length
at the beginning and end of the path, and then divide equally the remaining time for the
segments. (The fact that this re-parameterized path, whose image is still the same Kloosterman path, belongs to the support
is then an elementary consequence of the Weil bound for Kloosterman sums).
-
In general, the question is whether a given
has a reparameterization with Fourier coefficients (rather, those of
) are all smaller than
. This is an intriguing problem, and looking into it brought us into contact with some very nice classical questions in Fourier analysis, that I discuss in this later post. We only succeeded in proving the existence of a suitable reparameterization for real-valued functions, for reasons explained in the aforementioned later post, and it is an interesting analysis problem whether the result holds for all functions. A positive answer would in particular settle another natural question that we haven’t been able to handle yet: is there a space-filling curve in the support of the Kloosterman paths?
All this is great analytic fun. But there are nice arithmetic consequences of our result. By the definition of the support, we know at least that any has the property that, with positive probability, the actual path of the partial sums of the Kloosterman sums will come as close as we want (uniformly on
) to
, and this is an arithmetic statement. For instance, simply because the zero function belongs to the support, we deduce that, for a large prime
, there is a positive proportion of
such that all partial sums
for , have modulus
.
In other words, there is a non-zero probability that all the normalized partial sums of the Kloosterman sums are very small. (It is interesting to note that this is emphetically not true for character sums… the point is that their Fourier expansion involves multiplicative coefficients, so they cannot become smaller than .)