Bagchi’s Theorem is a functional version of earlier results of Bohr and Jessen related to the statistical properties of the Riemann zeta function on a vertical line between the critical line and the region of absolute convergence. It seems that it is not as well-known as it could, partly because Bagchi proved it in his thesis, and did not publish a paper with this result (his only related paper explicitly states that he removed the probabilistic language that a referee did not like). It seems therefore useful to describe the result. I will then sketch the proof I gave last semester…
Consider an open disc 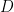 contained in the region
contained in the region 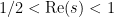 (other compact regions may be considered, for instance an open rectangle). For any real number
(other compact regions may be considered, for instance an open rectangle). For any real number 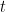 , we can look at the function
, we can look at the function 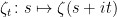 on
on 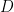 . This is a holomorphic function on
. This is a holomorphic function on 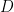 , continuous on the closed disc
, continuous on the closed disc 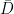 . What kind of functions arise this way? Bagchi proved the following (this is essentially Theorem 3.4.11 in his thesis):
. What kind of functions arise this way? Bagchi proved the following (this is essentially Theorem 3.4.11 in his thesis):
Theorem. Let 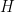 denote the Banach space of holomorphic functions on
denote the Banach space of holomorphic functions on 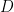 which are continuous on the closed disc. For
which are continuous on the closed disc. For  , define a probability measure
, define a probability measure 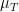 on
on 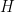 to be the law of the random variable
to be the law of the random variable  , where
, where 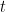 is uniformly distributed on
is uniformly distributed on ![[-T,T] [-T,T]](https://s0.wp.com/latex.php?latex=%5B-T%2CT%5D&bg=ffffff&fg=000000&s=0) . Then
. Then 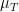 converges in law, as
converges in law, as  , to the random holomorphic function
, to the random holomorphic function
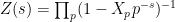 ,
,
where  is a sequence of independent random variables indexed by primes, all uniformly distributed on the unit circle.
is a sequence of independent random variables indexed by primes, all uniformly distributed on the unit circle.
This is relatively easy to motivate: if we could use the Euler product
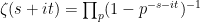
in 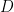 , then we would be led to an attempt to understand the probabilistic behavior of the sequence
, then we would be led to an attempt to understand the probabilistic behavior of the sequence 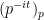 , viewed as a random variable on
, viewed as a random variable on ![[-T,T] [-T,T]](https://s0.wp.com/latex.php?latex=%5B-T%2CT%5D&bg=ffffff&fg=000000&s=0) with values in the infinite product
with values in the infinite product 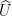 of copies of the unit circle indexed by primes. This is a compact topological group, and the easy answer (using the Weyl criterion) is simply that this sequence converges to the Haar measure on
of copies of the unit circle indexed by primes. This is a compact topological group, and the easy answer (using the Weyl criterion) is simply that this sequence converges to the Haar measure on 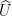 . In other words, the random sequence
. In other words, the random sequence  converges in law to a sequence
converges in law to a sequence  of independent, uniform, random variables on the unit circle. Then it is natural to expect that
of independent, uniform, random variables on the unit circle. Then it is natural to expect that 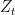 should converge to the random function
should converge to the random function 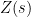 , which is obtained formally by replacing
, which is obtained formally by replacing  by its limit
by its limit  .
.
Bagchi’s proof is somewhat intricate, in comparison with this heuristic justification, especially if one notices that if 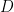 is replaced by a compact region in the domain of absolute convergence, then the same idea applies, and is a completely rigorous proof (one need only observe that the assignment of an Euler product
is replaced by a compact region in the domain of absolute convergence, then the same idea applies, and is a completely rigorous proof (one need only observe that the assignment of an Euler product
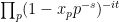
to a sequence 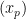 of complex numbers of modulus one is a continuous operation in the region of absolute convergence.)
of complex numbers of modulus one is a continuous operation in the region of absolute convergence.)
The proof I give in my script tries to remain closer to the basic intuition, and is indeed less involved (it avoids both a use of the pointwise ergodic theorem that Bagchi required and any use of tightness or weak-compactness). It makes it easy to see exactly what arithmetic ingredients are needed, beyond the convergence in law of 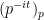 to the Haar measure on
to the Haar measure on 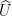 . Roughly speaking, it goes as follows:
. Roughly speaking, it goes as follows:
- One checks that the random Euler product
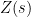 does exist (as an
does exist (as an 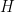 -valued random variable), and that it has the Dirichlet series expansion
-valued random variable), and that it has the Dirichlet series expansion
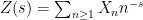
converging for  almost surely, where
almost surely, where  is defined as the totally multiplicative extension of
is defined as the totally multiplicative extension of 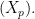 This is done as Bagchi did using fairly standard probability theory and elementary facts about Dirichlet series.
This is done as Bagchi did using fairly standard probability theory and elementary facts about Dirichlet series.
- One shows that
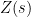 has polynomial growth on vertical lines for
has polynomial growth on vertical lines for  . This is again mostly elementary probability with a bit of Dirichlet series theory.
. This is again mostly elementary probability with a bit of Dirichlet series theory.
-
Consider next smoothed partial sums of
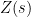 , of the type
, of the type
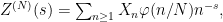
where 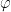 is a compactly supported test function with
is a compactly supported test function with  . Using again standard techniques (including Cauchy’s formula for holomorphic functions), one proves that
. Using again standard techniques (including Cauchy’s formula for holomorphic functions), one proves that
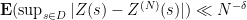
for some 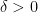 .
.
- One next shows that the smoothed partial sums of the zeta function
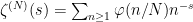
satisfy
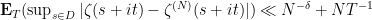
(the second term arises because of the pole), where 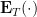 denotes the expectation with respect to the uniform measure on
denotes the expectation with respect to the uniform measure on ![[-T,T] [-T,T]](https://s0.wp.com/latex.php?latex=%5B-T%2CT%5D&bg=ffffff&fg=000000&s=0) . This step is also in Bagchi’s proof, and is essentially the only place where a specific property of the Riemann zeta function is needed: one requires the boundedness on average of
. This step is also in Bagchi’s proof, and is essentially the only place where a specific property of the Riemann zeta function is needed: one requires the boundedness on average of  in vertical strips to the right of the critical line. The standard proof of this uses the Cauchy inequality and the mean-value property
in vertical strips to the right of the critical line. The standard proof of this uses the Cauchy inequality and the mean-value property
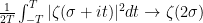
for any fixed 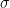 with
with 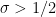 . It is here that the bottleneck lies if one wishes to generalize Bagchi’s Theorem to any “reasonable” family of
. It is here that the bottleneck lies if one wishes to generalize Bagchi’s Theorem to any “reasonable” family of  -functions.
-functions.
- Finally, we just use the definition of convergence in law: for any continuous bounded function
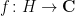 , we should prove that
, we should prove that
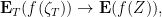
where 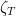 is the
is the 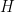 -valued random variable giving the translates of
-valued random variable giving the translates of  , and
, and  is the random Dirichlet series. The minor tweak that is useful to notice (and that I wasn’t consciously aware of before) is that one may assume that
is the random Dirichlet series. The minor tweak that is useful to notice (and that I wasn’t consciously aware of before) is that one may assume that 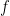 is Lipschitz: there exists a constant
is Lipschitz: there exists a constant 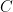 such that
such that

(this is hidden in standard references — e.g., Billingsley’s — in the proof that one may assume that 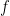 is uniformly continuous; the functions used to prove this are in fact Lipshitz…).
is uniformly continuous; the functions used to prove this are in fact Lipshitz…).
Now pick some parameter 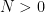 , and write
, and write
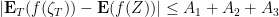 ,
,
where
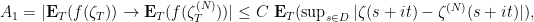
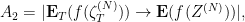
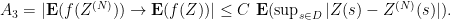
Fix 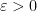 . For some fixed
. For some fixed 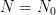 big enough,
big enough, 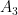 is less than
is less than  by Step 3, and
by Step 3, and  is at most
is at most  . For this fixed
. For this fixed  ,
,  tends to
tends to  as
as  tends to infinity because of the convergence in law of
tends to infinity because of the convergence in law of  to
to  — the sum defining the truncations are finite, so there is no convergence issue. So for all
— the sum defining the truncations are finite, so there is no convergence issue. So for all  large enough, we will get
large enough, we will get