If, like me, you consider yourself a “serious” ( ™ ) arithmetician, you may also have started spurning at an early age the type of numerical coincidences, sometimes found in dictionaries of remarkable numbers, that state that, for instance, is the only integral solution to the equation
However, maybe I shouldn’t be so dismissive. Today, after a discussion with P-O Dehaye, which was certainly serious enough since the Ramanujan function featured prominently, the question came to understand the solutions in
of the system
(everything modulo ).
This sounds rather innocuous, but something I find rather amusing happens: you can check for yourself that the solutions are either (i) diagonal (all are equal) or (ii) a permutation of
(i.e., no two
coincide). Why is that? Well, first both (i) and (ii) do describe solutions. Clearly (( ™ ) again) there are
solutions in total; there are
diagonal ones, and
permutations; since
there can be no other solution.
Is there a more direct proof?
Given a solution in which two of the are equal, permute it so that they are the first two terms and translate it so that they are both zero (the solutions are invariant under the translation
are equal, permute it so that they are the first two terms and translate it so that they are both zero (the solutions are invariant under the translation 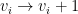 ). Then
). Then  , but this is easily seen to be impossible.
, but this is easily seen to be impossible.
(The group of solutions has a huge group of symmetries. There are commuting actions of and
and 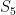 , that I can see.)
, that I can see.)
(Er, the set of solutions.)
Nice! (Though of course it’s not just the equation v_2^2+v_3^2+v_4^2=0 that has no non-trivial solutions — it does, e.g., (0,1,2) –, it is the system of this equation with v_2+v_3+v_4=0).