Today’s terminological post will be a contribution to the French-led insurgency that tries to replace the denomination “smooth number” (or “smooth integer“) with the much better “friable number” (in French, “nombre friable” instead of “nombre lisse“).
Of course, many readers may wonder “what is this anyway?”. And part of the point is that the better choice may lead such a reader to guess fairly accurately what is meant (possibly with a hint that this has to do with multiplicative properties of integers), whereas playing a game of “Define a smooth number” with a wide group of mathematicians may probably lead to wildly different interpretations.
So here is the definition: a positive integer n is called y-friable (or smooth, if you still insist) if all the prime divisors of n are at most y. The idea is that y should be much smaller than n, so that this means (intuitively) that n only has “small” prime factors. But the definition makes sense for all y, and for instance, any integer n is n-friable, a 2-friable integer is a power of 2, etc.
I do not wish to discuss the properties of those integers (only their name), so let me just refer to this survey by Granville for a discussion of their basic properties and of their applications to computational number theory.
The adjective “friable” (Capable of being easily crumbled or reduced to powder, OED) seems perfect to describe this type of integers: it is evocative and conveys not only something of the technical definition, but also a lot of the intuitive meaning and applicability. The other contender, “smooth”, has several problems (in fairness, it has at least one positive aspect: whatever we call them, the integers without large prime factors are extremely useful in many parts of analytic and algorithmic number theory, and the underlying current that smoothness is something desirable is not usurped): (1) it is much too overloaded (search for “smooth” without more precision in Math Reviews: 68635 hits as of tonight; for “friable”, only 19); (2) whichever meaning of smooth you want to carry from another field, it does not really mean anything here; (3) not to mention that, chronologically speaking, the terminology was already preempted by the smooth integers of Moerdijk and Reyes, which are the solutions of the equation sin π x=0 in the real line of suitable topoi (such as the smooth Zariski topos, apparently).
The chronology of the use of these words, as it appears from Math Reviews at least, seems quite interesting: the first mention it finds of “smooth numbers” in the number-theoretic meaning is in the title of a paper of Balog and Pomerance, published in 1992. However, the notion is of course quite a bit older: the standard paraphrase was “integers without large prime factors”, with many variants (as can be seen from the bibliography of Granville’s survey, e.g, A. A. Buchstab, “On those numbers in an arithmetic progression all prime factors of which are small in order of magnitude”, 1949; Balog and Sarkozy, “On sums of integers having small prime factors, I”, 1984; Harman, “Short intervals containing numbers without large prime factors”, 1991; etc : clearly, something needed to be done…).
As for “friable”, the first number-theoretic use (interestingly, the six oldest among the 19 occurences of “friable” in Math Reviews also refer to other contexts than number theory, namely some studies of models of friable materials, from 1956 to 1987) is in a review (by G. Martin in 2005) of a paper of Pomerance and Shparlinski from 2002, though “smooth” is used instead in the paper. The first occurence in a paper (and so, possibly, in print) is in one by G. Tenenbaum and J. Wu, published in 2003. It must be said that, for the moment, only French writers seem to use the right word (Tenenbaum, de la Bretèche, Wu, and their students)… G. Martin consistently uses it in his reviews, despite having to recall that this is the same as smooth numbers; however, he uses “smooth” in the title and body of his paper on friable values of polynomials (published in 2002, admittedly, and the abstract on his web page uses mostly “friable” instead…).
I agree that the terminology “smooth” is not intuitive.
But “friable”, in English, seems to mean “able to be fried”, even if that’s not the sense in which it’s intended. So to me, at least, there should be a corresponding verb “to fry”; what would this mean? If the insurgency succeeds, it wouldn’t surprise me if the verb “fry”, in the appropriate circles, became a synonym
for the verb “factor”.
I’ve also heard “round” as a term for numbers without large prime factors, but this seems to collide with the colloquial usage of “round” to mean numbers with decimal expansions ending in many zeroes. (Of course, the two concepts overlap; the latter just gives a special place to numbers with lots of factors of 2 or 5.)
Well, according to the OED, “friable” only means what I mentioned (“Capable of being easily crumbled or reduced to powder”), well-established with the first citation in 1563. There is no mention of a “fryable” there, but Google finds some in the sense of “able to be fried”, written “fryable”.
I think “round number” is quite bad for this notion, if it is used (I have not heard it myself; MR shows at least one recent paper of Hensely where a y-round number is really one which has y prime factors — something quite different).
I agree as another native speaker: “friable” is terrible. It is an extremely obscure word (I vaguely think I may have heard of it before, but I’ve certainly never seen it used) that really sounds like it has to mean “capable of being fried”. If it is used in number theory, then anyone who uses the term will have to spend time explaining that it has nothing to do with frying. Only someone with an exceptional vocabulary could guess what it meant without having to look it up.
I actually think “smooth” is a great choice, although maybe the intuition is a little too specific to me. I think of it like gravy: smooth gravy has no lumps or chunks in it, and the analogue of lumps for integers is big prime factors. :-)
Another disadvantage of “friable” is that it is a little awkward. It has three syllables and just is a little slow and clumsy to pronounce, while “smooth” sounds much better.
I don’t have the impression that “friable” is particularly obscure (all sources I have indicate it is much more commonly used than “fryable”), but one could of course replace it with another translation of the original French word, e.g., “brittle”, or “crumbly”.
[The previous comment seems to assume that anyone doing number theory is a “native speaker”, presumably an English speaker, but maybe I’m just overinterpreting… just in case, let me point out that this assumption is not valid…]
Sorry, I didn’t mean to suggest that everyone is a native speaker of English, just that I was, as evidence that I had a good feeling for what typical speakers would consider an obscure word. Michael Lugo was the other person I was indicating when I said I was “another”.
After looking into it more carefully, I agree that “friable” is pretty widespread in certain areas (such as gardening – about half of all online references to it mention soil). However, it’s still a word that few people would recognize unless they happen to be interested in one of those areas.
“Brittle” has the disadvantage of being a negative trait.
“Crumbly” sounds funny (no English word containing “umbl” sounds serious).
I like the sound of “frangible” more than “friable” and it avoids the issue of sounding like “fryable” to those who’ve never heard the word.
How about “fissile”? It’s also an obscure word as far as everyday use goes, but it is probably familiar to mathematicians because of its use in physics. I like the analogy of factoring to splitting the atom better than the other analogies (breaking glass or crumbling a cookie).
Well, it seems that my intuition about my native language is “wrong”, in the sense that there doesn’t seem to be textual support for it. I can accept that. However, I suspect that I am not the only native speaker of English who will, at least at first, think “friable” means “able to be fried”.
The terminology of “round” to mean “having only small prime factors” may be my own invention, now that I think about it. I like the terminology but would not use it without explanation.
There’s always the possibility of pronouncing “friable” with a heavy French accent, which would sound like “free-able”, and is unlikely to have anyone think of frying…
Just stumbled onto this blog by chance (great work Emmanuel, and I like the css too). I agree with other posters that “friable” is awkward (though I don’t share the linguistic anguishes of our fried-food aficionado); it is quite clearly a Gallicism: whilst technically being an acceptable translation of the French “friable”, it lacks its immediate intuition simply because it isn’t the obvious choice for the immediate experience of “friabilité”. Much better, in my opinion, would be “brittle”. I would claim that “brittle” is actually the most accurate translation of “friable” within the context suggested by numbers whose primes crumble off in small bits…
It is, after all, a familiar phenomenon that the etymologically most related translation is not the semantically closest (to wit, many ugly Anglicisms in French mathematics).
Brittle anyone?
–Nicolas
I like “friable” and would certainly not read it as “able to be fried.” But I would take Emmanuel’s suggestion of French-accenting the word further and prononunce it “free-ah-bluh.”
I agree with the consensus that “friable” is not a common word. According to the web companion for _Word Frequencies in Written and Spoken English_, it occurs 0 times per million words (rounded).
Another issue not mentioned: the definitions don’t match.
y-smooth integers are those where all prime divisors of n are at most y. Tenenbaum defines friable integers as those where all prime power divisors of n are at most y.
Sure, “friable” is not so common, but after all much of mathematical terminology has the same feature; and “smooth” is among those words which are so common that the confusion can become intense (one can probably imagine a dialogue among mathematicians where they both use it and only after a while does one realize that they are speaking of entirely different things).
As for the non-matching of the definitions, I’m puzzled: maybe once Tenenbaum did use the word in the sense you mention with powers of primes, but he certainly does not now: e.g., his last two papers with “friable” in the title
this one in English
and
this one in French
define “y-friable” in the first paragraph in the same sense as y-smooth.
I found the terminology in his last (English) published paper on the subject: “Integers with a large friable component” (2006). It’s on the first page. I’m accustomed to “smooth” and “powersmooth” to describe the two concepts.
I looked up the frequencies (same source) for the other mathematical terminology on the same page of the English paper you mention. (This way you know I’m not just cherry-picking common terms.) Here are the results (per million, rounded):
prime: 121
factor: 150
algorithm: 8
function: 129
parameter: 17
infinity: 3 (18 including various forms)
positive: 83
linear: 13
binary: 9 (probably much higher now)
integer: 4
irreducible: 1
real: 227
(Of course feel free to pick a different corpus or a different paper and try this yourself.)
So it does seem to be unusually rare. Of course math does use unusual terminology at times; after searching for an example (not in the paper), I see that “elliptic” also has a frequency of 0 (1 if you include ellipse).
As I read the 2006 paper, Tenenbaum only defines there the “y-friable component” of an integer n (as the product of those exact prime powers dividing n where p is at most y), and doesn’t recall what is a y-friable integer (at least not in the first page). This definition (of y-friable component) is consistent with it being the largest y-friable divisor of n, if the meaning of a y-friable integer is the standard y-smooth one.
You’re right about component vs. integer, sorry about glossing over that.
But the y-friable component of an integer N is *not* the largest y-friable integer dividing N. The 4-friable component of 120 is 3, while the largest 4-friable integer dividing 120 is 24.
One may of course define any mathematical term as one wishes, but Tenenbaum’s paper states
“Given an integer n and a real parameter y, we define
to be the y-friable component of n.”
This gives n_4=24 for n=120 (and I think most analytic number theorists would consider this to be the right definition).
(This is compatible with speaking of the p-component of an integer, etc).
Oops! I misread that. Sorry.
I don’t see why “fine” isn’t used. I remember that in Munkres the concept of a finer/coarser topology gets explained using language that is almost identical to this. Friable is nice if you’re familiar with it but it’s very obscure (I worked as a gardener for a few months and never heard it) and it sounds weird, either as Fry-a-bull or Free-ab-luh.
I think that “crumbly numbers” is by far the best translation. I shall use that from now on.
Bonjour,
J’ai une question pas si évidente que cela et dont je ne trouve la réponse nulle part :
1 est-il un nombre 2-friable ?
(et 3-friable, etc. Je suppose que 0 n’est pas un nombre friable puisque tous les entiers le divisent.)
Quand on parle d’entier friable, implicitement, il s’agit d’entiers strictement positifs, comme dans la plupart des questions en théorie multiplicative des nombres. Pour déterminer la réponse à ce type de question, on peut simplement regarder la série de Dirichlet génératrice; pour les entiers -friables (ou
-friables (ou 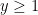 ), on veut que ce soit
), on veut que ce soit  (produit partiel de la fonction zêta de Riemann), et on voit donc que le nombre 1 est
(produit partiel de la fonction zêta de Riemann), et on voit donc que le nombre 1 est  -friable…
-friable…