The harmonic series and surrounding folklore

Speaking of divergent series, I’d like to mention one of my favorites bits of informal folklore: this starts with a slogan

The only “truly” divergent series is the harmonic series
$H=1+\frac{1}{2}+\cdots +\frac{1}{n}+\cdots,$

which, of course, deserves plenty of quotes. But the idea is quite sound: it is that, given about any other series with real or complex terms (which does not involve this one in a hidden manner, of course, e.g., as an “irreducible summand”), such as

$\sum_{m\geq 1}{(-1)^{m+1}\frac{m^2}{4m^2-1}},$

it is quite often possible, by some kind of trick or feint, to assign a “value” (i.e., a real or complex number) to the series in a way which is reasonable and useful for certain purposes. [A famous example is the (apparently) ultra-divergent series

$\sum_{m\geq 0}{(-1)^m m!}=1-1+2-6+24-120+720-\cdots,$

which was considered by Wallis and Euler: its “value” is

$e\int_0^1{e^{-1/x}x^{-1}dx}=e\int_1^{+\infty}{y^{-1}e^{-y}dy}=0.5963473623231\ldots$

(see this article for an explanation of some of Euler’s ideas to do this “computation”).]

One setting in which the philosophy above has been refined to a precise (conjectural) statement is the theory of L-functions (over number fields). Indeed, observe that (formally) we have

$H=\zeta(1),$

where ζ(s) is the Riemann zeta function, which is only defined properly for the real part of s larger than one by the series

$\zeta(s)=\sum_{n\geq 1}{\frac{1}{n^s}}.$

Then, after translating the basic insight about the harmonic series from Dirichlet series to L-functions, one gets the following folklore conjecture:

If a reasonable (say, automorphic, or “motivic”) L-function L(s) over a number field k has a pole at s=1 (when normalized so that the functional equation relates values at s and 1-s), then L(s) is divisible by the Riemann zeta function, in the sense that
$L_1(s)=\frac{L(s)}{\zeta(s)}$
does not acquire poles at any of the complex zeros of the Riemann zeta function.

This is quite a rich problem: it contains a famous conjecture of Artin (the Dedekind zeta function of a number field should be divisible by the Riemann zeta function), and applied to the Rankin-Selberg convolution, it suggests the existence of the symmetric-square L-functions of modular forms — indeed, the first crucial result towards the “automorphic” existence of the latter (due to Gelbart and Jacquet), was the proof of this divisibility property by Shimura).

Now for the most amazing thing concerning this folklore property (at least to me): it seems that it also works modulo primes! Let me explain this (an explanation which I heard from Jean-Pierre Serre): another renowned formula of Euler for the values of the zeta function at even integers can be rephrased, after using the functional equation

$\pi^{-s/2}\Gamma(s/2)\zeta(s)=\pi^{-(1-s)/2}\Gamma((1-s)/2)\zeta(1-s),$

as the formula

$\zeta(1-2n)=1+2^{2n-1}+3^{2n-1}+\cdots + k^{2n-1}+\cdots =-\frac{1}{2n}B_{2n},$

where the Bernoulli numbers B_2n are rational numbers defined by the power series expansion

$1-\frac{1}{2}x+\sum_{n\geq 1}{B_{2n}\frac{x^n}{n!}}=\frac{x}{e^x-1}$

(and, of course, the middle expression for ζ(1-2n) is purely formal: it is one more example of a divergent series that can be given a convincing value).

The idea now is that the last expression (-1/2n B_2n) can be reduced modulo a prime p, provided p does not divide 2n and does not divide the denominator of the Bernoulli number. Now, lo and behold, the primes dividing the denominators of Bernoulli numbers are known: they are exactly the primes such that

$p-1\mid 2n$

or equivalently such that

$k^{2n-1}\equiv k^{-1}\text{ mod } p$

for all integers k coprime with p (those for which the inverse modulo p makes sense…). So the Bernoulli number can not be reduced modulo primes exactly when (either p divides 2n or) formally we have

$-\frac{1}{2n}B_{2n}\equiv 1+2^{2n-1}+3^{2n-1}+\cdots + k^{2n-1}+\cdots\equiv 1+2^{-1}+\cdots +k^{-1}+\cdots,$

the divergent harmonic series again! (One must omit the terms with k divisible by p of course, but since this is purely formal, why not?).

I have no idea if there is a good explanation for this coincidence, but it is remarkably beautiful, and it certainly gives a convincing argument for the fact that the numerators of Bernoulli numbers are much more mysterious: so are the zeros of the Riemann zeta function, in comparison with its pole…)

Dear Emmanuel,

As you probably know, the divergent congruence that you mentioned at the end
of your post is related to the Kubota-Leopoldt p-adic L-function (which
is a p-adic interpolation of the rational
special values of the zeta function).

More precisely, this function interpolates
the values (1-p^k) times zeta(k), for negative odd integers k. (The above product exactly “strips away” the Euler
factor at p in zeta(k), the phenomenon
you already observed in your mod p harmonic series.)

The interpolation is as follows: the variable k should be thought of as a
character of the units in Z_p, i.e. of
Z_p*, namely the character x maps to x^k.
Note that k and k’ are close, when thought of as characters of Z_p* in this sense, when k is congruent to k’ modulo (p-1) times a big power of p.

The p-adic L-function is then defined
on the space of all characters, except
for a simple pole at the identity character (i.e. at k = 1). What this means is that if k is close to 1,
i.e. (k-1) is divisible by (p-1) times
a big power of p, then the value of the p-adic L-function will have a big power
of p in its denominator, i.e. (since (1-p^k) is a p-adic unit), the value zeta(k) will have a big power of
p in its denominator.

Writing k = 1 – 2n, we then see that
B_{2n}/2n should have p in the denominator
when p-1 divides 2n, as you observe; and
this power of p will indeed be larger if 2n is also divisible by a big power of p.

Incidentally, if p divides the numerator
of B_{2n}, then the value of the p-adic L-function at k = 1 – 2n is divisible
by p, i.e. is congruent to 0 mod p, and
a theorem of Ferero-Washington (vanishing
of the mu-invariant) implies that there
is in fact a zero of the p-adic L-function
congruent to k mod (p-1).

This theory is the analytic side of Iwasawa theory. On the algebraic side,
one has a vast generalization of Kummer’s
classical theory of cyclotomic fields (and
in particular, of the theory of irregular
primes in Kummer’s sense), culminating in Mazur and Wiles’ proof of the Main Conjecture of Iwasawa Theory, which relates the algebraic and analytic
sides of the story. (One can think
of it as an enormous generalization of
Kummer’s criterion for a prime to be
irregular in terms of divisibility of
Bernoulli numbers.)

Regards,

Matthew

4 thoughts on “The harmonic series and surrounding folklore”

Tom says:

19.11.2008 at 13:50

I think the last part of your post is related to the so-called Giuga-Agoh conjecture which says that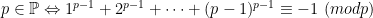 $p\in\mathbb{P}\Leftrightarrow 1^{p-1}+2^{p-1}+\dots+(p-1)^{p-1}\equiv -1\ (mod p)$ , but I can’t really spell out how.
Blair S says:

19.11.2008 at 17:49

This Giuga-Agoh conjecture looks partly related to Fermat’s Little Theorem. i.e.

p \in \mathbb{P} \Rightarrow a^{p-1} \equiv 1 (\mbox{mod p}) ; a < p \Rightarrow \sum_{a=1}^{p-1}{a^{p-1}} \equiv \sum_{a=1}^{p-1}{1} \equiv -1 (\mbox{mod p}) \\
Matthew Emerton says:

20.11.2008 at 7:22

Dear Emmanuel,

As you probably know, the divergent congruence that you mentioned at the end
of your post is related to the Kubota-Leopoldt p-adic L-function (which
is a p-adic interpolation of the rational
special values of the zeta function).

More precisely, this function interpolates
the values (1-p^k) times zeta(k), for negative odd integers k. (The above product exactly “strips away” the Euler
factor at p in zeta(k), the phenomenon
you already observed in your mod p harmonic series.)

The interpolation is as follows: the variable k should be thought of as a
character of the units in Z_p, i.e. of
Z_p*, namely the character x maps to x^k.
Note that k and k’ are close, when thought of as characters of Z_p* in this sense, when k is congruent to k’ modulo (p-1) times a big power of p.

The p-adic L-function is then defined
on the space of all characters, except
for a simple pole at the identity character (i.e. at k = 1). What this means is that if k is close to 1,
i.e. (k-1) is divisible by (p-1) times
a big power of p, then the value of the p-adic L-function will have a big power
of p in its denominator, i.e. (since (1-p^k) is a p-adic unit), the value zeta(k) will have a big power of
p in its denominator.

Writing k = 1 – 2n, we then see that
B_{2n}/2n should have p in the denominator
when p-1 divides 2n, as you observe; and
this power of p will indeed be larger if 2n is also divisible by a big power of p.

Incidentally, if p divides the numerator
of B_{2n}, then the value of the p-adic L-function at k = 1 – 2n is divisible
by p, i.e. is congruent to 0 mod p, and
a theorem of Ferero-Washington (vanishing
of the mu-invariant) implies that there
is in fact a zero of the p-adic L-function
congruent to k mod (p-1).

This theory is the analytic side of Iwasawa theory. On the algebraic side,
one has a vast generalization of Kummer’s
classical theory of cyclotomic fields (and
in particular, of the theory of irregular
primes in Kummer’s sense), culminating in Mazur and Wiles’ proof of the Main Conjecture of Iwasawa Theory, which relates the algebraic and analytic
sides of the story. (One can think
of it as an enormous generalization of
Kummer’s criterion for a prime to be
irregular in terms of divisibility of
Bernoulli numbers.)

Regards,

Matthew
Kowalski says:

20.11.2008 at 7:26

Thanks for the detailed explanation! I’ve once read some pages about p-adic zeta and L-functions (and I’ve heard the basic terminology, if only during lectures, so I should probably have guessed that the explanation for whatever I was discussing lied there…), but it’s never really entered into my mindset.

Comments are closed.

Published by

Kowalski

4 thoughts on “The harmonic series and surrounding folklore”