I have one more lecture next week in my expander class, but today I finished the proof of Helfgott’s growth theorem for 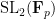 . As I had hoped, I did this in my notes with explicit constants (I didn’t try to follow those constants on the blackboard).
. As I had hoped, I did this in my notes with explicit constants (I didn’t try to follow those constants on the blackboard).
Taking into account some grains de sel, since there may well be minor computational mistakes lurking around (though I have already corrected a few), the result I obtain is the following: if 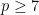 is prime, and if
is prime, and if  is a symmetric generating set, containing
is a symmetric generating set, containing 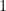 for simplicity, then either the triple product
for simplicity, then either the triple product
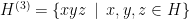
is all of 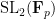 , or otherwise we have
, or otherwise we have
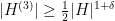
where
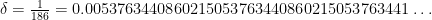
(Of course, the factor  can be incorporated into a slightly-smaller exponent, but that introduces an ugly-looking dependency on the size of
can be incorporated into a slightly-smaller exponent, but that introduces an ugly-looking dependency on the size of 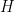 , which one must recover using an uglier trivial bound for
, which one must recover using an uglier trivial bound for 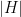 small, so I preferred this version…)
small, so I preferred this version…)
The current version of the notes contains the argument, though it is a bit rough (I will soon rearrange some of it, to attempt to provide more motivation — at least the way I understand how it goes…)
For the proof, I followed the clear outline in the first sections of the paper of Pyber and Szabó. This reduces the problem, rather quickly and cleanly, to a “non-concentration” estimate for the intersection of 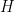 with a regular-semisimple conjugacy class
with a regular-semisimple conjugacy class 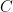 , of the type
, of the type
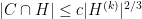
for some fixed 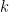 and absolute constant
and absolute constant  . This inequality is now commonly called a (generalized) Larsen-Pink inequality (the prototype going back to the late 90’s preprint — now published — of Larsen and Pink for the non-concentration of finite subgroups of algebraic groups in subvarieties). Though the general case is quite tricky, there is here an easy enough argument, based on studying the fibers of the map
. This inequality is now commonly called a (generalized) Larsen-Pink inequality (the prototype going back to the late 90’s preprint — now published — of Larsen and Pink for the non-concentration of finite subgroups of algebraic groups in subvarieties). Though the general case is quite tricky, there is here an easy enough argument, based on studying the fibers of the map
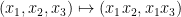
where the three arguments  are all in
are all in 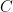 (this is the basic idea already presented by Larsen and Pink to explain their result, in another case).
(this is the basic idea already presented by Larsen and Pink to explain their result, in another case).
It turns out that, if one imposes that 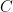 is not the conjugacy class of elements of trace 0, which can be ensured (using bare hands) by “escape from subvarieties”, the cases where this map has positive-dimensional fibers are rather simple to analyze (I owe this computation to R. Pink…)
is not the conjugacy class of elements of trace 0, which can be ensured (using bare hands) by “escape from subvarieties”, the cases where this map has positive-dimensional fibers are rather simple to analyze (I owe this computation to R. Pink…)
Moreover, only one case requires another instance of Larsen-Pink-type inequalities (those readers who have looked at the paper of Larsen and Pink, or the one of Breuillard-Green-Tao which has a general “approximate” version, will know that there is a rather complicated induction involved in general), and it is a very easy one: if 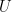 is the subgroup of upper-triangular unipotent matrices, then
is the subgroup of upper-triangular unipotent matrices, then
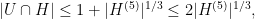
which is an instructive exercise. (In fact, in rearranging this section of my notes, I will use this as a motivating example…)
With this final ingredient, I can now produce (with the same amount of salt…) an effective spectral gap for the Cayley graphs of the Lubotzky subgroup of  , generated by
, generated by
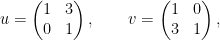
modulo primes, namely (drumroll) for  large enough (drumroll; but I won’t tell you how large today), we have (drumroll)
large enough (drumroll; but I won’t tell you how large today), we have (drumroll)
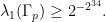
(Actually, I already know various points of inefficiency in my treatment of the Bourgain-Gamburd expansion argument which should lead to some improvements, and I hope to find other avenues to explore and stones to turn to do better…)