Mathematics – Page 62 – E. Kowalski's blog

Projection to subspaces and a theorem of Chebychev

I just taught at ETH the basic result of the theory of Hilbert spaces that states that, given such a space H, a vector v in H and a closed, non-empty, convex subset C, there exists a unique vector y in C such that

$||v-y||=\inf_{w\in C}{||v-w||},$

and which deserves to be called the orthogonal projection of v on C, as the picture tries to illustrate:

Having done this, I looked for counterexamples to illustrate that this natural statement does not extend to the Banach space setting; it is easy enough to find situations where the minimum is achieved more than once (in fact, infinitely often), but slightly more challenging to find one where the minimum is not achieved at all. Here is one (it was in one of the books I use for my course): consider the Banach space c₀ of sequences (indexed by n>0) of complex numbers converging to 0, with the sup norm

$||(u_n)||=\sup_{n\geq 1}{|u_n|}.$

Consider then the linear map

$\lambda(u)=\sum_{n\geq 1}{2^{-n}u_n}$

on c₀. It is clear that this is a continuous linear map since it is bounded by 1 on the unit ball, and a moment’s thought shows that in fact we have

$|\lambda(u)|<1\quad\text{ if } \quad ||u||\leq 1$

because equality would require that u be a constant sequence, and this is impossible if the sequence is to converge to zero, except (of course) when the constant is zero, but then λ(0)=0 anyway….

This is a case where a supremum is not achieved, and so it is easily transformed to what we want by taking, e.g., v=0 and the convex set

$C=\{v\in c_0\,\mid\, \lambda(v)=1\}.$

Then there does not exist a vector in C minimizing the distance to the origin.

Now, this is probably not too surprising to anyone, but while preparing these counterexamples for exercises for the students of my course, I was reminded of a beautiful approximation result of Chebychev which is probably not well-known (outside the numerical analysis community, where it seems to be standard knowledge) and which gives a particular (important) case outside of the Hilbert space context where the minimization process works.

Consider the (real) Banach space B of real-valued continuous functions on [0,1] with the supremum norm (i.e., the norm of uniform convergence of functions). Fix then a degree d>0. In B, the subspace Pol_d of real polynomials of degree at most d is a closed (non-empty) convex subset. The approximation problem is therefore, for a given continuous function f, to find the polynomials P of degree at most d which minimize the distance to f:

$||f-P||=\sup_{0\leq x\leq 1}\ \ |f(x)-P(x)|$

must be equal to

$D_d=\inf_{P\in \text{Pol}_d}{||f-P||}.$

It is not very difficult to prove the existence of at least one such polynomial P (the idea being to show that the minimization can be restricted to a compact subset of the subspace Pol_d). It is more difficult to prove unicity, and even more subtle to find the following characterization (which was found by Chebychev): a polynomial P (of degree at most d) is the best approximation to f in this sense if and only if, there exist at least d+2 points, say

$x_1<x_2<\ldots<x_n,\quad n\geq d+2,$

such that

$|f(x_i)-P(x_i)|=||f-P||,\quad\text{ for all } i,$

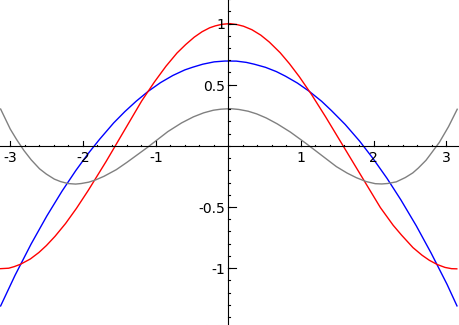
and moreover the signs of f(x_i)-P(x_i) alternate when i increases. Below, I call the existence of points with these two properties the “d+2 alternation property”; note that it says nothing about the size of the distance from f to P. Here is an illustration:

the red function f is the cosine function, and the blue graph is the best approximation of degree (at most) 3; the gray line is the difference cos(x)-P(x), and the 5 alternating extrema are clearly visible. (I used Maple to construct the approximation, and Sage to plot the graph).

The unicity seems to be typically proved by first showing that there is at most one polynomial with the d+2 alternation property (which is fairly easy; in fact, alternation with d+1 points would be enough), and then showing that minimizing polynomials are characterized by it. The most technical part is the proof that a minimizing polynomial has the required property (if there are less than d+2 alternations, one shows how to improve the approximation).

But the converse (an alternating polynomial is minimizing) looks also quite difficult at first since, as we observed, the defining condition doesn’t say anything about the size of

$||f-P||,$

only that it is achieved at d+2 points. But here is the trick: suppose another polynomial Q (of degree at most d) is such that

$(*)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ||f-Q||<||f-P||.$

Then, at the points x_i, the difference Q-P has the same sign as f-P (by writing

$Q(x_i)-P(x_i)=(f(x_i)-P(x_i)) - (f(x_i)-Q(x_i)),$

and the second summand is not big enough, by (*), to provoke a change of sign). By the assumption of alternation of signs of the d+2 values

$f(x_i)-P(x_i),$

(which hasn’t been used yet), this means the polynomial Q-P, of degree at most d, has at least d+1 changes of signs, hence that many zeros, so we must have Q=P, which is a contradiction.

Incidentally, the only reason I know this result is that it was the subject of one of the entrance exams at the French École Polytechnique, and that this exam text was (because of this) used by the teacher of my Math. Spé for one of our weekly take-home exams; the last questions were set up in a challenging way (which I don’t remember, but it must have been the proof of the clever part above), and the result was fixed in my mind because I succeeded in finding the trick…

For a full account, see for instance Analysis of Numerical Methods, by Isaacson and Keller (which I only have in my personal library because it was in the bargains bin in the English bookstore in Bordeaux one day, for some mysterious reason).

Reading Buffon, I

I’ve started reading the volume of Buffon’s Histoire Naturelle where the Buffon needle problem is discussed, partly out of curiosity (why is it called Essai d’arithmétique morale? why is it included in a book of natural history?) and partly, I must say, because the book’s format is remarkably convenient to put in a coat pocket and read while travelling in the Zürich tramways. (It’s certainly much easier to carry along than any modern scientific book I’ve ever seen).

A few pages suffice to understand the meaning of the title and, at least, why probability theory is related. Buffon is interested here in various types of “truths” or “certainties” (vérités et certitudes, in French). In fact, he distinguishes three kinds: (1) intellectual (geometric or mathematical) certainties; (2) physical certainties; and (3) moral certainties, and the discussion of the third kind is really the topic of his essay (and probably it is indeed the most original — of course I am not knowledgeable about his possible precursors here, but whereas I could recognize at least partly his ideas on the first two kinds of truths, I do not remember encountering something similar to the third one before).

Geometric certainties, for Buffon, are those of mathematics. He states that there is not much to be said about them, because they refer, or derive, ultimately, from accepted truths (axioms, though I didn’t see the word in the text) using obvious rules of inference (… (elles) se réduisent toutes à des vérités de définition). In effect, he takes the point of view (which I’ve seen in other places) that mathematics, properly considered, is tautological and really should be trivial, except if irrelevant or badly-posed questions are raised. (I’ll probably come back to this, and other mathematical topics in the essay, because there are amusing remarks there).

Physical and moral truths are different because they refer to the “real” world. The distinction between the two is that a typical physical certainty is that “the sun will rise tomorrow”, which is knowledge based on experience and considered to be “true” because it has been verified in a very large number of cases, going back to the beginning of the world. Moral certainties, on the other hand, are based on much less data, and are more a matter of personal conviction and analogies.

Where things really become interesting is when Buffon decides to quantify these two types of truths, which are not absolutely certain, by assigning a numerical probability to them — indeed, this is were probability theory comes in. Geometric certainties have absolute probability (l’évidence n’est pas susceptible de mesure), being immune to any kind of doubt. But Buffon says that physical certainties are not absolute, rather they are those which have a probability comparable to that of the sun rising tomorrow (puisque le Soleil s’est toujours levé, il est dès-lors physiquement certain qu’il se lèvera demain). The latter, he estimates rather curiously, by (implicitly) assigning the probability 1/2 to each event “the sun rises” on any given day, and assuming that those events are independent. Since, he says, the sun has risen every day for about 6000 years (!), the probability of the negation of a physically certain event is about

$2^{-6000\cdot 365+1}=2^{-2189999},$

and hence it is zero for any practical purpose. (It’s not clear what Buffon really thinks of this estimate of the age of the earth; he remarks that 2000 more years would not change anything to the qualitative feature of this bound, but doesn’t go further).

Now for moral certainties, things are much more interesting. Buffon states that he considers that a good estimate for the probability of the negation of a “morally certain” event is the probability p that a person, aged 56 years old and in good health, will die within the next twenty four hours. He argues that this is a correct value because people typically dismiss this probability by going about on their normal activities every day. So, he says, if some other event has probability less than p, it can be considered to be morally impossible, and therefore should be dismissed from consideration in any practical matter. (Or comme tout homme de cet âge, où la raison a acquis toute sa maturité, & l’expérience toute sa force, n’a néanmoins nulle crainte de la mort dans les vingt-quatre heures … j’en conclus que toute probabilité égale ou plus petite, doit être regardée comme nulle…)

Then Buffon goes about finding a value for p. For this, he has very detailed and scrupulous mortality tables and statistics (about 350 pages at the end of this volume, in fact), and from this he concludes that p is of size roughly 1/10189 (which he rounds up to 1/10000; note that “homme” means “person” in his discussion, since the mortality tables he uses do not distinguish between men and women). There is then an interesting footnote (click on the image below to see it on the right-hand page), where he informs the reader of the comments of Daniel Bernoulli on this matter: Bernoulli is said to have approved of the principle, but objected that the correct value should be 1/100000 instead, because one should take into account that sick people are included in the statistics, and are likely to be much more afraid of dying on a given day.

After establishing this value of p, more developments follow of how knowing this could (or should) affect people’s actions, and in particular a long discussion involving gambling, which is mathematically rather weird — so I’ll discuss it in the next post… (Readers may also, of course, still be wondering what the needle has to do with any of this…)

(Note: The tables at the end make for melancholy reading; Buffon observes that

One fourth of the human race perishes, so to say, before having seen the light, since about a quarter dies within the first eleven months of life… A third perishes, before the age of twenty three months, that is to say, before having had the use of their limbs, and of most of their other organs…

There is no indication that he thinks these numbers to be anything but “moral certainties” (he calls them vérités) — facts of life, that will not change during the course of humanity’s existence on Earth.)

Buffon’s needle

As a result of recent moves, the (almost) complete set of Buffon’s monumental Histoire naturelle belonging to my father’s family has recently arrived here in Zürich (it comes from my grand-father, who was director of the Muséum d’histoire naturelle de Nantes). I will keep these in my office for the moment, as it definitely lends it a very scholarly air…

(As far as I can see from the web page above, what is missing from our set is the Histoire naturelle des poissons, which was not written by Buffon anyway, but by the Comte de Lacépède, who also wrote the volumes about snakes, which we do have).

Many probabilists know Buffon for his annoying habit of dropping needles on the parquet, and finding the value of π after doing this sufficiently many times. This game was indeed included in his natural history, more precisely in the Essai d’arithmétique morale (or “Essay of moral arithmetic”) in Volume VII of the Suppléments — at least, it is there in my family’s edition, though it is missing from the web site containing Buffon’s works, where the Essai is in Supplement volume 4.

Here are pictures of the first pages of the description of the problem (click for readable larger picture):

and

Notice the delightful typography and orthography: the “s” that looks like an integral sign (and is barely distinguishable from an “f”), the way the past tense is written demanderoit instead of the current demanderait, etc.

Some things I didn’t know about groups

Experimenting with finite groups recently, I’ve learnt a few things I was completely unaware of:

(1) there are so many distinct groups of order 512 (or 1024, 1152, 1536 and 1920) up to isomorphism, that Magma and GAP are not able to recognize them (they have databases of groups of order up to 2000, except for 1024, but given one abstract group of this order, they can not pinpoint which element of the database it is). Precisely, there are 10494213 distinct finite groups of order 512 up to isomorphism, 157877 of order 1152, 408641062 of order 1536 and 241004 of order 1920. These numbers are several order of magnitude larger than what I would have guessed if asked point-blank.

(2) the order of groups of a fixed Lie type, say X(q), where X could be PSL, is not always monotonic with respect to the variable q; for instance:
gap. Order(PSL(3,17)); 6950204928 gap. Order(PSL(3,19)); 5644682640 gap. Order(PSL(3,29)); 499631102880 gap. Order(PSL(3,31)); 283991644800

(Of course, this is then easy to check, and the point is that when q-1 is divisible by 3, the order drops as the center of SL(3,q) becomes a bit bigger).

Random matrices, L-functions and primes

This could be the title of a book, of a research paper, but it is really (for the current purpose) the name of the conference that Ashkan Nikeghbali (from Universität Zürich) and myself are organizing in late October — from October 27 to October 31, to be precise –, thanks to the support of the Forschungsintitut für Mathematik from ETH Zürich.

Despite the late announcement, this has been in preparation for a few months already, but we are both not always the most efficient among organizers. However, there is at last some kind of web page, although for the moment it is not really more informative than the poster that will soon be printed and distributed everywhere (click for full-size picture):

The chameleon in the picture, in case you are wondering, is one specimen from the Zürich rainforest. It has no special meaning apart from that.

(The following

almost became the poster, but it was finally decided that the other one was more memorable).

We hope that this conference will be an occasion to further the links between probability theory and number theory, in particular through the three topics of the title.