Mathematics – Page 61 – E. Kowalski's blog

A long computation: the Chebotarev invariant of the Rubik’s group

Motivated by a recent post on God Plays Dice concerning the maximal order of elements in the Rubik’s group (the permutation group that describes the movements of the divine cube), I of course decided to try to compute how many conjugacy classes in it you typically need to know to generate the whole group — in other (self-coined) words, I decided to entrust to Magma the computation of the Chebotarev invariant of this group of order 43252003274489856000.

After two days of hard work on my desktop computer, Magma gave the following answer: the expectation of the waiting time is 5.6686453… and the expectation of the square is 36.7870098… (giving a standard deviation slightly larger than 2). This is actually the longest individual computation I’ve performed myself, and it took about 1 Gb memory; computing the 20 conjugacy classes of maximal subgroups was done in about 1.3 seconds, computing the 81120 conjugacy classes took 45 seconds more, and then precomputing the matrix indicating which subgroups intersected which conjugacy class was roughly one day long, the second day being devoted to the alternating sum over the 2²⁰-1 non-empty subsets of maximal subgroups (with the formula indicated at the end of my original post defining the Chebotarev invariant) — this is about one million steps.

The computation was done with floating point numbers with 30 digits precision, but I think the last 10 or so are not to be trusted (and I did not write them down), since they come from this alternating sum with a million terms (but I would trust the first 15, say, because the summands are rationals, hence the approximations used for individual terms are really correct to 30 digits).

A characterization of reflexive Banach spaces

As I continue teaching Functional Analysis, I am happily learning new things, which typically come out of trying to think how to present the material in a way that motivates it for my students. I try to insert, at least at particularly important places, some example or indication that will give some understanding of why various steps (or constructions, or definitions) can be seen as natural ones. Often, this leads to natural questions which are not always explicitly mentioned or highlighted.

Here is one such situation: since I have started by treating Hilbert spaces, I try to present analogies and contrasts when it comes to Banach spaces. One such contrast, of course, involves the fact that Banach spaces are not always reflexive. What this means is that the natural (bi)duality map

$D\ :\ V\rightarrow V\prime\prime$

is not always surjective, where D is the linear map between a Banach space V and the dual of its dual space V”, given by defining D(v) as the linear functional

$D(v)\ :\ \lambda\mapsto \lambda(v)$

for all λ in the dual space.

For a Hilbert space V, the (or one of the) Riesz Representation Theorem gives essentially an identification of V with its dual (or rather the “conjugate” Hilbert space in the case of complex scalars), from which the surjectivity follows because, properly interpreted, D is simply the identity.

To start explaining this, and why it may fail, and what “reflexivity” means, I follow the following path, which is (hopefully) quite natural here, since it is based on the Hilbert space proof, but which turned out to not be really emphasized in the textbooks I am using as references.

First, the Riesz representation theorem is typically proved (and I proved it) using the general result of existence of a projection of a vector on a closed convex set, in particular on a closed linear subspace: given W a closed subspace of V, and a vector v in V, there exists a unique w such that

$||v-w||=\inf_{y\in W}{||v-y||}$

and in particular the infimum on the right is attained. For a general Banach space, this result is not always true, both in terms of unicity, and of existence. I will now concentrate on the latter property (see this earlier post for an example and another nice result involving this type of minimization problems).

I used the question of extending this type of results as a first motivating fact for the Hahn-Banach theorem: one of the first corollaries of it is that, for any vector v, we have

$(*)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ||v||=\max_{||\lambda||\leq 1}{|\lambda(v)|}$

where λ ranges over all elements of the dual space which have norm at most 1, i.e., such that

$|\lambda(x)|\leq ||x||$

for all vectors x. The content is first that there is equality with a sup on the right-hand side, but in addition that this supremum is attained.

It is now perfectly natural to wonder whether the “dual” identity

$(**)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ||\lambda||=\max_{||v||\leq 1}{|\lambda(v)|}$

holds, or in other words, whether a linear functional λ always attains its supremum on the closed unit ball of V (since the supremum is exactly ||λ|| by definition of the norm on the dual space).

That these are maxima instead of minima as in the previous case of Hilbert spaces is not particularly problematic, since one can always go from one to the other; in fact the counterexample mentioned earlier was exactly of this type: for a certain linear form, (**) was not correct, and a counterexample to the minimization problem followed straightforwardly.

However, it is very easy to see that (*) implies that (**) is true, for all linear forms on V, provided V is reflexive. So we get from the previous example a very straightforward proof, based on trying to understand the contrast between Hilbert and Banach spaces, that the space c₀ that occured is not reflexive.

But then one can ask (and I asked myself): is the converse to this implication true? In other words, assuming we have the nice property (**) for all continuous linear maps on V, does it follow that V is reflexive?

It turns out the answer is indeed Yes, but it seems to be a difficult result of Banach space theory. This is a theorem of R.C. James, and I found it mentioned (in a slightly disguised form) in Conway’s book on functional analysis, and following the reference, found the proof contained in this paper (Studia Mathematica, 1964). It is, indeed, by no means straightforward (though I am certainly not expert enough to really understand the proof after a first glance…).

None of the other texts I am looking at for my course mentions this (unless it escaped my notice, which is quite possible). Presumably, this is because it is not a particularly fruitful approach to further studies of Banach spaces (as the unbalance between both sides of the implication suggests), but it is definitely nice to know and to mention to students.

(One of my teachers once said — and I’m sure this has been said many times of many subjects — that “completely general facts in topology are either obvious or false”; this result indicates that the same clearly cannot be said of Banach spaces).

Dickson and Robinson

I’ve profited from the AMS Publisher’s Sale to finally buy Dickson’s History of the Theory of Numbers and the Collected Works of Julia Robinson (for, respectively, 37$ instead of 146$ and 19$ compared with 61$, both are very good bargains), and I’ve started browsing randomly around both texts.

Looking in Volume I of Dickson work (which deals more particularly with “multiplicative” number theory and prime numbers in particular), I was happy to find a reference for the cute proof that there exist infinitely many prime numbers that follows from the combination of the following two facts:

(1) Euler’s identities (dating to around 1730)

$\prod_{p}{\frac{1}{1-p^{-2}}}=\sum_{n\geq 1}{\frac{1}{n^2}}=\frac{\pi^2}{6},$

(2) Legendre’s theorem: π² is an irrational number (going back to around 1790).

I only heard this proof in 2005 (in a lecture by Iwaniec), and although I’ve asked a few people, no one seemed to know how far back this went. Dickson mentions an obscure survey of J. Braun in Wiss. Beilage Jahresbericht, Gymn. Trier, 1899, who

… attributes to Hacks a proof by means of Π(1-1/p²)^-1=Σs^-2=π²/6 …

(Chapter XVIII, page 414, of Volume I). Nothing is said here about who Hacks was, but he reappears on page 427 for a paper in Acta Mathematica of 1893, where he proved for instance that for a prime p, we have

$\sum_{y=1}^{p-1}\sum_{s=1}^{p-1}\left[\frac{ys}{p}\right]=((p-1)/2)^2(p-2),$

and moreover this is characteristic of primes. (He is also referenced in a few other places in Volume I for similar facts).

Of course, although somewhat pointless, this argument is “obvious” enough that is it possible (in fact, likely) that this was discovered independently many times. But at least, I’m happy to know that this was noticed a long time ago.

A few people have (also independently) wondered if this proof could be made quantitative. The idea is to use explicit measures of irrationality of ζ(2): for some constants C>0 and α, we have

$(*)\ \ \ \ \ \ \ \ \ \ \ \ |\zeta(2)-p/q|\geq Cq^{-\alpha}$

for all coprime integers p, q. Then we look at the numerators and denominators of the Euler product over primes < X, and compare the quality of the rational approximation obtained with what is permitted by (*) (the best known version of this holds with α=5.441243…, due to Rhin and Viola).

This is also clearly art for art sake, but amusing facts emerge. First, the known arguments leading to (*) use information about primes, typically of the same quality as the Chebychev bounds. Thus the argument is dangerously close to circular, because the consequences are typically weaker! However, Miller, Schiffman and Wieland have looked at the arguments of Rhin and Viola and played cleverly with it to obtain non-circular consequences about the distribution of primes. The second amusing fact is that it is in a sense much better to prove that there are infinitely many primes using the irrationality of

$\frac{1}{\zeta(2)}=\prod_{p}{(1-p^{-2})}=\prod_{p}{\frac{p^2-1}{p^2}},$

because the denominator is not as hard to control: this was the idea of J. Sondow (although he didn’t deduce any explicit consequence, it follows that using an irrationality measure one gets

$\pi(X)\gg \log\log X,$

which my own trial only produced by appealing to Linnk’s theorem on the size of the smallest prime in an arithmetic progression — a much deeper theorem than even Chebychev’s bound!)

As for Julia Robinson, I am not even an amateur logician, and I don’t understand her purely logical works, but she is renowned for works that mix logical ideas and number-theoretic results, and these may be appreciated without much logical background.

Her contributions to the solution of Hilbert’s 10th Problem are probably the best known, but not far from this is her remarkably beautiful characterization of the integers as a subset of the rationals in the language of first order theory of rings. In other words, what she found was a logical formula φ(x), with one free variable x, involving only addition, multiplication, 0, 1, and the logical connectors “and”, “or”, “not” and quantifiers “for all” and “there exists” (which are interpreted as ranging only over variables restricted to the rationals), such that, given a rational number x, the formula φ(x) is “true” (with the standard interpretation of the various logical constructs) if and only if x is in fact an integer.

This is not easy at all; in fact, here is the formula in her original work (part of her PhD thesis; there may, of course, be simpler versions known today):

$\forall a,b\ (\{\psi(a,b,0)\ \text{and}\ \forall m\ [\psi(a,b,m)\rightarrow \psi(a,b,m+1)]\}\rightarrow \psi(a,b,x))$

where ψ(a,b,n) is the formula

$\exists x,y,z\ (2+abn^2+bz^2=x^2+ay^2).$

Proving that it does what it is supposed to do involves some substantial number theory (namely, the Hasse principle for quadratic forms in three variables with rational coefficients), but is a beautiful elementary argument apart from that.

Inaugural lecture

A nice tradition of ETH Zürich (and some other institutions) is the inaugural lecture that newly hired members of the faculty give to describe to a large audience some of their research topics (indeed, the lectures are open to the general public). I just gave my own Einführungsvorlesung, entitled “The art of sieving”. The actual lecture can be seen online, but it may also be interesting to have a look at the full beamer presentation, since I ended up presenting only about three-quarters of what I had prepared, and some of the most interesting things (at least, the closest to current research) were located towards the end. (Precisely, I stopped at the end of page 74 of the PDF).

Of course, my lecture does not compete — in terms of sheer viewability value — with the presentation on Monday of Marc Pollefeys, who showed the current state of the art of 3D reconstruction of objects and scenes using (2D) video and pictures, or with the (possibly apocryphal) inaugural lecture of P. L. Nageoire for the Chaire d’études des alcools forts of Collège de France.

I still hope that some of the excitement of studying primes will come through. Encouragingly, two colleagues who are now retired, and who were not previously working in “Pure” Mathematics told me during the Apéro afterwards that they are happy to study prime numbers now as a hobby, and had liked my lecture.

Relations betweens roots of polynomial equations

It does not seem to be so well-known that there can be only very few linear relations between the roots of an irreducible polynomial which has a “large” Galois group (in a certain sense, which is made clearer below). For instance, given a monic polynomial P in Q[T], written

$P(T)=T^d+a_{d-1}T^{d-1}+\cdots+a_1T+a_0,$

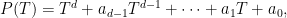
it is easy to create a polynomial Q of the form

$Q(T)=T^d+b_{d-2}T^{d-2}+\cdots+b_1T+b_0$

whose roots generate the same field. If β_i are the roots of Q, the vanishing of the coefficient of T^d-1 means that they satisfy the Q-linear relation

$\beta_1+\cdots+\beta_d=0.$

If the Galois group of the splitting field of Q (or P) is the full symmetric group on d letters, then in fact this is the only possible relation (up to multiplication by a fixed scalar)!

In other words, it is impossible, for instance, that the roots α_i of P satisfy

$\alpha_1-\alpha_2+\cdots +(-1)^d\alpha_d=0,$

$\alpha_1+2\alpha_2+\cdots +d\alpha_d=0.$

Proving this type of fact can be seen either as a fun exercise in the representation theory of finite groups, or as a good way of motivating its usefulness. (The basic knowledge needed is the existence of decomposition into irreducibles, and unicity of the isotypical space corresponding to a given irreducible representation; the treatment by J-P. Serre is probably the clearest introduction).

Indeed, if the question was presented to a student in the form of showing that either of the previous two relations are incompatible with the α_i being roots of a polynomial with symmetric Galois group G=S_d, it is likely that it would be natural to expand the hypothetical relation by stating that, for any σ in G, we have (for the last case, say):

$\sigma(\alpha_1)+2\sigma(\alpha_2)+\cdots +d\sigma(\alpha_d)=0.$

If the Galois group is indeed S_d, we can choose σ so that

$\sigma(\alpha_1)=\alpha_2,\ \sigma(\alpha_2)=\alpha_1$

and the other roots are fixed; then subtracting the new relation from the first one, we get

$-\alpha_2+\alpha_1=0,$

which is impossible.

This was particularly easy, but to refute the possibility of all relations (except the sum of the roots being 0), something more systematic is needed. The type of argument used suggests to consider the vector space of all possible relations:

$R=\{(\lambda_1,\ldots,\lambda_d)\,\mid\,\lambda_1\alpha_1+\cdots+\lambda_d\alpha_d=0\}$

and the basic idea is that G acts on R by its action on the roots, in other words, R is a linear representation of G (over C, or a smaller field if one wants).

If we then take the point of view of trying to identify this representation among the representations of G, we are naturally led to remark that it is defined as a subrepresentation of the permutation representation of G acting on the roots

$F=\bigoplus_{1\leq i\leq d}{\mathbf{C}\cdot [\alpha_i]},\text{ with } \sigma([\alpha_i])=[\sigma(\alpha_i)],$

which, as a representation, doesn’t depend on the particular polynomial (and its roots), but only on the group G, as a transitive permutation group acting on d objects.

So, for any particular transitive group G acting on d objects, one can construct the representation F, decompose it into sums of irreducibles π_i (this is a problem of group theory), and then it follows that R can only be isomorphic to a direct sum of those representations occuring in R, with multiplicities at most equal to that in F: if

$F\simeq n_1\pi_1\oplus\cdots \oplus n_k\pi_k,\ \text{ with } n_i\geq 1,$

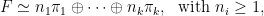
then R can only be of the form

$R\simeq m_1\pi_1\oplus\cdots \oplus m_k\pi_k,\ \text{ with }\ 0\leq m_i\leq n_i.$

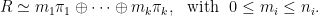
Then one can look at each possibility in turn, and try to see which ones can actually occur as relations of roots of a polynomial. This is clearly easiest if F has few summands, particularly if there is no multiplicity (i.e., if each n_i is 1), for then the subspace corresponding to a summand that occurs in R must be equal to that in F, which is itself uniquely determined.

[If there is multiplicity, say n₁=2, then in the π₁-isotypic component F₁ in F, there are infinitely many subspaces isomorphic to π₁, with multiplicity one, for instance

$V_{\lambda}=\{(v,\lambda v)\,\mid\,v\in V\}$

for each (fixed) scalar λ, where V is a fixed subspace of F₁, G stable and isomorphic to π₁ under this action. Each of these subspaces can lead to different relations.]

In the case of the symmetric group, the decomposition of the natural permutation representation is well-known:

$F=\mathbb{1}\oplus \pi$

where 1 is the subspace generated by

$[\alpha_1]+\cdots +[\alpha_d]$

while the complement subspace

$\pi=\{(\lambda_1,\ldots,\lambda_d)\,\mid\, \sum_{i}{\lambda_i}=0\}$

is irreducible. Then, 1 is in R precisely when the sum of the roots is zero (and we already know that this possibility can occur), and π can not be (contained in) a relation module, because in particular

$(1,-1,0,\ldots,0)\in \pi$

which leads (as before, but now in full generality) to the absurd relation

$\alpha_1=\alpha_2.$

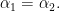
In my paper on relations between zeros of zeta functions over finite fields, I applied this method to understand the possible additive relations (and the multiplicative ones, using the same technique with the module of multiplicative relations instead of R) when the Galois group is the Weyl group of Sp(2g). Here also the situation was simple, with three summands in F, each with multiplicity 1.

In fact, experimenting with Magma, I can see that most transitive permutation groups of small degree seem to have the property of not having multiplicity in the permutation representation. The first counter-example is the symmetric group S₃, acting on itself by multiplication (there is no multiplicity in the natural action on three letters); indeed, if G acts on itself by multiplication, the permutation representation is isomorphic to the regular representation, and each irreducible occurs with multiplicity equal to its dimension, so such a transitive action always has multiplicity if the group is non-abelian. But most transitive groups are given with an action on a smaller set, and one finds that among the 173 non-trivial transitive groups of degree at most 11, only 5 exhibit some multiplicity. (Note that it is not clear at all if this impression can be quantified precisely).

This type of problem has been investigated a lot by K. Girstmair, and this paper of his (in Acta Arithmetica, 1999) is probably the most complete introduction to the subject.