Mathematics – Page 40 – E. Kowalski's blog

Pocket Kloostermania

It has been well said that Kloosterman sums are everywhere. Back in August, I showed how to visualize them on an ordinary laptop or desktop computer — software available also on its own page.

However, modern enlightened thought holds that availability on even the smallest of netbooks is not a good measure of ubiquity. Hence, without further ado, I am happy to introduce Pocket Kloostermania, the Android version. An installable package file can be downloaded from this link; it, and the source code, are also available now on the Kloostermania page; the license remains GPLv2.

Here’s what it looks like on the emulator.

Features/user manual are:

* The program has been installed and tested only on a Nexus One; it probably requires at least Android 2.0, but should be adaptable to earlier ones.

* On startup, the program displays the graph for S(1,1;173).

* Changes of orientation of the screen are recognized.

* Pressing the Menu soft key brings three choices (as seen on the picture):

Modulus and sum

New sum

Done

Back

About

More Cauchy distribution

I’ve mentioned earlier the first cases I had found of (almost) mod-Cauchy convergence (see this post for the definition).

Yesterday, following from a citation in Sarnak’s note to one in a paper of Guivarc’h and Le Jan, I ended up looking at this paper of F. Spitzer, which implicitly proves a true mod-Cauchy convergence result. Morever, this result is very interesting from the probabilistic point of view, since it concerns that most beautiful of objects, the (complex) Brownian motion.

Here is the result: consider such a complex Brownian motion

$W(t)=W_1(t)+iW_2(t),$

for non-negative t, where the real and imaginary parts are themselves independent standard Brownian motions on the real line, except that the real part is started at

$W_1(0)=R,$

for some fixed R> 0 (for instance R=1).

Because almost surely the Brownian motion is not zero, one can define a continuous process

$\theta_R(t)=\mathrm{Im} \log W(t),\quad\quad \theta_R(0)=0,$

which measures the argument of the Brownian motion and its winding around the origin. Spitzer’s result is then the fact that

$\frac{\theta_R(t)}{\log \sqrt{t}}$

converges in law, as t goes to infinity, to a Cauchy distribution with parameter 1 (it had already been noticed by P. Lévy that the argument of the Brownian motion is not square-integrable).

However, his argument is more precise: using relations with suitable PDE’s, he manages to compute exactly the Fourier transform of the law of the argument in terms of Bessel functions: for u≥0 (this characteristic function is even), we have

$\mathbf{E}(e^{iu\theta_R(t)})=\sqrt{\frac{\pi R^2}{8t}}e^{-R^2/(4t)}\Bigl\{I_{(u-1)/2}\Bigl(\frac{R^2}{4t}\Bigr)+I_{(u+1)/2}\Bigl(\frac{R^2}{4t}\Bigr)\Bigr\}$

where I_ν(x) is the I-Bessel function of index ν.

Since the first term in the power series expansion (at 0) of the Bessel function is given by

$I_{\nu}(x)=\frac{(x/2)^{\nu}}{\Gamma(\nu+1)}+O(x^{\nu+1}),$

it follows easily that we have a mod-Cauchy convergence:

$\exp(A(t)|u|) \mathbf{E}(e^{iu \theta_R(t)})\longrightarrow \Phi(u),$

as t goes to infinity, with parameters and limiting function given by

$A(t)=\log\frac{\sqrt{8t}}{R},\quad\quad \Phi(u)=\frac{\sqrt{\pi}}{\Gamma((|u|+1)/2)}=\frac{\Gamma(1/2)}{\Gamma((|u|+1)/2)}.$

The computation of Salié sums

I’m continuing preparing my notes for the course on exponential sums over finite fields, and after the fourth moment of Kloosterman sums, I’ve just typed the final example of “explicit” computation, that of the Salié sums, which for the prime field Z/pZ are given by

$T(a,b;p)=\sum_{1\leq x\leq p-1}{\Bigl(\frac{x}{p}\Bigr)e\Bigl(\frac{ax+bx^{-1}}{p}\Bigr)},$

(the (x/p) being the Legendre symbol, and e(z)=exp(2iπ z) as usual in analytic number theory). These look suspiciously close to Kloosterman sums, of course, but a surprising fact is that they turn out to be rather simpler!

More precisely, we have the following formula if a and b are coprime with p (this goes back, I think to Salié, though I haven’t checked precisely):

$T(a,b;p)=T(a,0;p)\quad \sum_{y^2=4ab}{e\Bigl(\frac{y}{p}\Bigr)},$

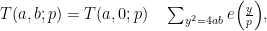
the inner sum running over the solutions of the quadratic equation in Z/pZ. The first term is simply a quadratic Gauss sum, which is well-known to be of modulus

$|T(a,0;p)|=\sqrt{p},$

and since the inner sum contains either 0 or 2 terms only, depending on the quadratic character of a modulo p, we get trivially the analogue

$|T(a,b;p)|\leq 2\sqrt{p}$

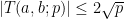
of the Weil bound for Kloosterman sums.

The standard proof of this formula is due to P. Sarnak. It is the one which is reproduced in my earlier course on analytic number theory and in my book with H. Iwaniec. However, since it involves a somewhat clever trick, I tried a bit to find a more motivated argument (motivated does not mean motivic, though one can certainly do it this way…).

I wasn’t quite successful, but still found a different proof (which, of course, is very possibly not original; I wouldn’t be surprised, say, if Sarnak had found it before the shorter one in his book). The argument uses a similar trick of seeing the sum as value at 1 of a function which is expanded using some discrete Fourier transform, but maybe the function is less clever: it is roughly

$x\mapsto T(xa,b;p)$

instead of something like

$x\mapsto T(x^2a,b;p),$

(and it uses multiplicative characters in the expansion, instead of additive characters). It’s a bit longer, also less elementary, because one needs to use the beautiful Hasse-Davenport product formula: denoting

$\tau(\chi)\quad=\quad\sum_{0\leq x\leq p-1}\quad \chi(x)e\Bigl(\frac{x}{p}\Bigr)$

the Gauss sums associated with multiplicative characters, we have

$\tau(\chi)\ \tau(\chi\ (\frac{\cdot}{p})) = \overline{\chi(4)}\ \tau((\frac{\cdot}{p}))\ \tau(\chi^2),$

which is the analogue for Gauss sums of the duplication formula

$\Gamma(s)\Gamma(s+1/2)=2^{1-2s}\Gamma(1/2)\Gamma(2s),$

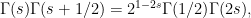
for the gamma function. Since this formula is most quickly proved using Jacobi sums (the analogues of the Beta function…), which I had also included in my explicit computations of exponential sums, using this argument is a nice way to make the text feel nicely interlinked and connected. And it’s always a good feeling to use a proof which is not just the same as what can be found already in three of four places (at least when you don’t know those places; for all I know, this may have been published twenty times already).

Now, you may wonder what Salié sums are good for. To my mind, their time of glory was when Iwaniec used them to prove the first non-trivial upper bound for Fourier coefficients of half-integral weight modular forms (this is the application Sarnak included in his book), which then turns out to lead quite easily (through some additional work of W. Duke) to results about the representations of integers by ternary quadratic forms. Another corollary of Iwaniec’s bound, through the Waldspurger formula and Shimura’s correspondance, was a strong subconvexity bound for twisted L-functions of the type

$L(1/2,f\times \chi)$

where f is a fixed holomorphic form and χ is a real Dirichlet character, the main parameter being the conductor of the latter.

The point of Iwaniec’s argument was that the Weil-type bound, when applied to the Fourier coefficients of Poincaré series, which can be expressed as a series of Salié sums

$T(m,n;c)$

(with fixed m and n) in the half-integral weight case, just misses giving a result. So one must exploit cancellation in the sum over those Salié sums, i.e., as functions of the modulus c. This is hopeless, at the moment, for Kloosterman sums, but the semi-explicit expression for the Salié sums in terms of roots of quadratic congruences turns out to be sufficient to squeeze out some saving…

(Nowadays, there is a wealth of techniques to directly prove subconvexity bounds for the twisted L-functions — e.g., in this paper of Blomer, Harcos and Michel –, and one can run the argument backwards, getting better estimates for Fourier coefficients from those; as is well-known, one finds this way that the “optimal” bound for the Fourier coefficients is equivalent with a form of the Lindelöf Hypothesis for the special values…)

The fourth moment of Kloosterman sums

One of my favorite computations is that of the fourth moment of Kloosterman sums:

$M_4=\sum_{1\leq a,b\leq p-1}{|S(a,b;p)|^4}=(p-1)(2p^3-3p^2-3p-1),$

where

$S(a,b;p)=\sum_{1\leq x\leq p-1}{\exp(2i\pi (ax+b\bar{x})/p)},\quad\text{where}\quad x\bar{x}\equiv 1\text{ mod } p.$

This was almost first performed with spectacular consequences by H.D. Kloosterman himself in 1927, as a crucial step to proving an upper bound for his sums, which was sufficiently good for his application to representations of integers by integral positive definite quadratic forms in four variables (I recommend reading at least the introduction to this paper: it is strikingly modern).

I say almost, because after just checking his paper, I realized he just got the right order of magnitude, and not the exact formula, for M₄.

The standard reference I had been using (including for the exam of a graduate course I taught a while ago…) was in Iwaniec’s delightful book on classical modular forms. (Kloosterman sums appear there because, as in fact already noticed by Poincaré in 1912, they occur in the formulas for Fourier coefficients of Poincaré series…) But while typing the result for my lecture notes of my new course on sums over finite fields, I worked out a different argument than the one in Iwaniec’s book (different but, it turns out, rather closer to Kloosterman’s own…).

Roughly, one first quickly reduces (using orthogonality of additive characters) to computing the number of solutions of the equations

$x_1+x_2=y_1+y_2,\quad 1/x_1+1/x_2=1/y_1+1/y_2,\quad x_i,\ y_i\in \mathbf{F}_p^{\times}.$

This can be computed quite directly, as Iwaniec does, but one can also observe that there are obvious solutions

$(x_1,x_2,x_1,x_2),\quad (x_1,x_2,x_2,x_1),$

and wonder what others can exist? It is then fairly natural to try to see whether knowing

$(x_1+x_2,1/x_1+1/x_2),$

is enough to recover the pair (x₁,x₂), up to permutation. This will be the case, if we can compute the value of the product x₁ x₂ from the two symmetric quantities above (this is the theory of symmetric functions, in a rather trivial case). Now, observe the identity

$x_1x_2=\frac{(x_1+x_2)}{(x_1^{-1}+x_2^{-1})},$

which gives what we want, provided (of course) the denominator is non-zero. And indeed, this may of course vanish, and does so precisely for the extra solutions

$(x_1,-x_1,y_1,-y_1)$

of the original equations… The argument therefore proves there are no other than these three families, and after figuring out their intersections, the formula for the fourth moment follows. (Details are in my ongoing notes already mentioned above…)

This computation may seem desperately low-brow; however, as I discuss briefly in Section 6 of my most recent survey on applications of the Riemann Hypothesis over finite fields (I tend to like writing about this, I must confess…), this can be interpreted, via the “Larsen alternative” as the crucial step in proving the vertical (or average) Sato-Tate Law for Kloosterman sums: if we write

$S(1,a;p)=2\sqrt{p}\cos \theta_{a,p},\quad\quad \theta_{a,p}\in [0,\pi],$

then the collection of angles

$\{\theta_{p,a}\}_{1\leq a\leq p-1},$

becomes equidistributed with respect to the Sato-Tate measure

$\mu=\frac{2}{\pi}\sin^2\theta d\theta,$

as p goes to infinity…

[Update (27.2.2010): thanks to Ke Gong for sending some useful typographical corrections to the notes.]

Exponential sums over finite fields course

This semester, I am teaching (besides a course on Integration and Measure theory, about which I’ll write later) a course on elementary methods in the study of exponential sums over finite fields. The intent is to describe first the proof of the Riemann Hypothesis of A. Weil for one-variable exponential sums, based on Stepanov’s method (possibly in the version of Bombieri, possibly not), then go to more recent results where the “elementary” methods put to shame the cohomological formalism, e.g. Heilbronn sums or Mordell-type exponential sums involving polynomials with large degree (as in the work of Bourgain, though I haven’t yet quite settled on the detailed programme for that part of the course).

I’m hoping to type my lecture notes as I go along. In fact, the goal of the course is partly to prepare things both for a follow-up in the next semester on the cohomological approach and for a book I’ve been thinking about for quite a while on this topic. I don’t know what will come of this idea (for one thing, I’m starting slowly and as elementarily as I can, which is not really the style of the final book I have in mind, which would be a user guide for already fairly experienced analytic number theorists and other mathematicians interested in applying exponential sum methods to their own problems), and I doubt that even two semesters will be enough to lecture on what I wish to include, but the notes will be available on this page (together with links to various other documents of interest).