This is again the first of a series of a few posts in which I will explain (as promised a very long while ago, and as far as I can…) the trace weights that are used in my paper with É. Fouvry and Ph. Michel (henceforth, this paper will be referred-to as FKM). Given a prime number  , these are certain specific functions
, these are certain specific functions

that “come from algebraic geometry”, and that can be studied using both a very rich formalism, and such extraordinarily deep results as Deligne’s “Weil 2” form of the Riemann Hypothesis over finite fields.
In fact, each function of this type is really a kind of “shadow” of a more intrinsic (more algebraic, more geometric, more arithmetic, as you wish) object, and it is rather these objects which algebraic geometry studies. In general, 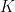 does not determine this other object: if I call
does not determine this other object: if I call 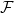 the latter, it may well be the case that two distinct objects
the latter, it may well be the case that two distinct objects  and
and 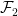 give rise to the same trace function
give rise to the same trace function 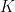 . However, there is also a basic complexity invariant
. However, there is also a basic complexity invariant  defined for a given
defined for a given 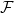 (which is called its “conductor”), and one can show (this uses the Riemann Hypothesis…) that, given
(which is called its “conductor”), and one can show (this uses the Riemann Hypothesis…) that, given  , there is a bound
, there is a bound  (which grows with
(which grows with  ) such that a given function
) such that a given function 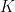 can come from at most one object
can come from at most one object 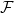 with complexity at most
with complexity at most  . I will come back to this in a later post, since I consider the question of determining precisely
. I will come back to this in a later post, since I consider the question of determining precisely  to be quite fundamental and fascinating, but for the basic purpose of FKM, this issue does not really arise.
to be quite fundamental and fascinating, but for the basic purpose of FKM, this issue does not really arise.
As a terminological aside, we tend to call these functions 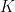 either “trace weights” or “trace functions”. Maybe a better word might be well-deserved for this notion, but we’re not quite sure what might work, though possibly we might use “tracic function”, a good translation of the French fonction tracique that we’ve found ourselves using; this has, at least, some classic ring.
either “trace weights” or “trace functions”. Maybe a better word might be well-deserved for this notion, but we’re not quite sure what might work, though possibly we might use “tracic function”, a good translation of the French fonction tracique that we’ve found ourselves using; this has, at least, some classic ring.
In this first post, I will outline the three possible definitions (or interpretations) of the class of trace functions, going from what is possibly the most closely related to notions known to analytic number theorists, and ending with the most flexible, but maybe least familiar one.
Special Hecke eigenvalues of automorphic forms. In the first picture, one looks at automorphic forms related to the field  of rational functions over the finite field
of rational functions over the finite field 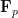 . As is the case for classical modular forms, there are Hecke operators associated to each place of
. As is the case for classical modular forms, there are Hecke operators associated to each place of 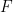 , in particular to the irreducible polynomials
, in particular to the irreducible polynomials  for
for 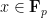 . Given an automorphic form
. Given an automorphic form  , one can then define a function
, one can then define a function

the corresponding Hecke eigenvalue for these particular Hecke operators. The complexity of  can then be defined as the sum of the “traditional” automorphic conductor and the rank
can then be defined as the sum of the “traditional” automorphic conductor and the rank  . Indeed, it is essential here to consider automorphic forms on all groups
. Indeed, it is essential here to consider automorphic forms on all groups 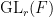 , and not just on
, and not just on 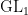 or
or  .
.
As examples, imitating the correspondance from Dirichlet characters to Hecke characters for 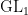 over the field
over the field 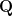 , it is not too difficult to construct explicitly some automorphic forms (of rank
, it is not too difficult to construct explicitly some automorphic forms (of rank 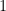 ) for which the associated functions are given by
) for which the associated functions are given by
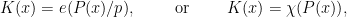
for some polynomial ![P\in\mathbf{Z}[X] P\in\mathbf{Z}[X]](https://s0.wp.com/latex.php?latex=P%5Cin%5Cmathbf%7BZ%7D%5BX%5D&bg=ffffff&fg=000000&s=0) and some multiplicative Dirichlet character
and some multiplicative Dirichlet character  . These are certainly the most natural-looking “functions of algebraic origin” on a finite field, and indeed this construction of (analogues of) Dirichlet characters is the original, and easiest, way to prove the rationality and functional equation for the associated
. These are certainly the most natural-looking “functions of algebraic origin” on a finite field, and indeed this construction of (analogues of) Dirichlet characters is the original, and easiest, way to prove the rationality and functional equation for the associated  -functions over
-functions over 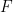 (since, in order to prove this, one does not even need to mention automorphic forms, the whole argument happening within the realm of Dirichlet characters.)
(since, in order to prove this, one does not even need to mention automorphic forms, the whole argument happening within the realm of Dirichlet characters.)
Despite their many fine qualities, automorphic forms are however a bit inflexible from the point of view of defining generalizations of these basic functions  . For instance, it is rather difficult to write down concretely the function attached to an automorphic form of rank at least
. For instance, it is rather difficult to write down concretely the function attached to an automorphic form of rank at least  . In fact, I don’t really know how to do it (except for automorphic forms built from the case
. In fact, I don’t really know how to do it (except for automorphic forms built from the case 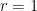 , like analogues of Eisenstein series) without first applying one of the two other definitions, constructing some object
, like analogues of Eisenstein series) without first applying one of the two other definitions, constructing some object 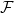 and associated trace function
and associated trace function 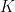 , and then invoking some version of the Langlands correspondence to claim the existence of some automorphic form
, and then invoking some version of the Langlands correspondence to claim the existence of some automorphic form  with Hecke eigenvalues
with Hecke eigenvalues 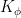 coinciding with the original
coinciding with the original 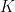 .
.
Similarly, given two functions  ,
, 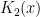 arising as Hecke eigenvalues of some automorphic forms
arising as Hecke eigenvalues of some automorphic forms  and
and 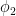 , it is a rather big theorem to show that there exists another automorphic form with eigenvalues
, it is a rather big theorem to show that there exists another automorphic form with eigenvalues
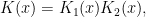
(for  unramified for both
unramified for both  and
and 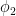 ): this is the general theory of the Rankin-Selberg convolution.
): this is the general theory of the Rankin-Selberg convolution.
Another serious drawback (which I will amplify later) is that this is — as far as I know, and at current time — strictly a one-variable story. There is no simple definition (that I know) that can be used to easily package a family of automorphic forms 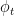 and, for instance, create a new automorphic form
and, for instance, create a new automorphic form 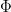 with Hecke eigenvalues related to some average of the eigenvalues of
with Hecke eigenvalues related to some average of the eigenvalues of 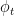 .
.
Galois representations of function fields. The first alternative to automorphic representation is given by Galois representations, and it is again a customary picture on the side of number fields. The base field is still  , but we now consider the Galois group
, but we now consider the Galois group
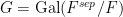
of some separable closure of 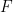 , and finite-dimensional representations
, and finite-dimensional representations
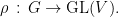
Then, as is customary in algebraic number theory, for any  , we have the associated decomposition and inertia group at the place corresponding to
, we have the associated decomposition and inertia group at the place corresponding to  , and the Frobenius automorphism
, and the Frobenius automorphism  which acts on
which acts on 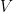 if
if  is unramified for
is unramified for  (i.e., if the inertia group at
(i.e., if the inertia group at  acts trivially on
acts trivially on 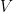 ) and which acts on the invariants
) and which acts on the invariants  otherwise. In all cases we can define a function
otherwise. In all cases we can define a function

It is immediately clear that such a definition gives a very flexible formalism, because we are now dealing largely with linear algebra. So formally, we can add these functions (taking direct sums of representations), multiply them (taking tensor product; because this operation does not always commute with invariants, the corresponding trace function coincides with the product of the two factors at the unramified  , but may differ at the others.) There is a non-trivial difficulty having to do with topology: to obtain a good theory, since
, but may differ at the others.) There is a non-trivial difficulty having to do with topology: to obtain a good theory, since 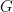 is an infinite profinite group, we want to consider continuous representations. But then, if
is an infinite profinite group, we want to consider continuous representations. But then, if 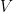 is a
is a  -vector space with its usual topology, we have the difficulty that there are too few representations: any continuous representation then has finite image. One works around this issue by the well-know device of picking some auxiliary prime number
-vector space with its usual topology, we have the difficulty that there are too few representations: any continuous representation then has finite image. One works around this issue by the well-know device of picking some auxiliary prime number  , and considering continuous representations into
, and considering continuous representations into 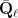 -vector spaces. There are many representations in that case (in particular, many with large infinite image), but of course the trace function now takes values in an
-vector spaces. There are many representations in that case (in particular, many with large infinite image), but of course the trace function now takes values in an  -adic field. Qu’à cela ne tienne (or, as Katz says, ell-adic, schmell-adic), one can pick (with some effort or help from a friendly axiom) an isomorphism
-adic field. Qu’à cela ne tienne (or, as Katz says, ell-adic, schmell-adic), one can pick (with some effort or help from a friendly axiom) an isomorphism

and consider the function
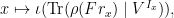
which is complex-valued.
The complexity is, here also, easy to define: there is a notion of Artin conductor for such a representation, and we add the dimension of 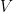 to take the latter into account.
to take the latter into account.
For applications to constructing interesting function, this business involving  shouldn’t be considered as too problematic. In fact, to a large extent, it turns out that the theory is rather independent of
shouldn’t be considered as too problematic. In fact, to a large extent, it turns out that the theory is rather independent of  . Without wanting to develop this too much, one can already see it by noticing that for any
. Without wanting to develop this too much, one can already see it by noticing that for any  , one can rather easily construct Galois representations with trace functions equal to
, one can rather easily construct Galois representations with trace functions equal to

the basic examples already considered. In fact, this is rather simpler than the corresponding construction of Dirichlet characters of 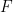 , and in particular, it is very easy to go from the construction of representations
, and in particular, it is very easy to go from the construction of representations  and
and 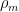 with respective trace functions
with respective trace functions

to the case involving a general polynomial: we have a map 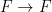 by
by  , hence a map of Galois groups
, hence a map of Galois groups 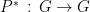 , and we can “just” consider the composites
, and we can “just” consider the composites

to get the desired representations. (This is really a restriction of representations.)
This theory also has fairly natural extensions to higher-dimensional varieties (though one must assume some smoothness for the theory to work decently). To a large extent, FKM might have been written in this language, as far as the definitions of trace weights are concerned. But we use instead the third approach…
Middle-extension sheaves on the affine line. This last theory is closer in terms of formalism to the previous one, but more geometric in spirit, and it is the most flexible. Indeed, it is the one we use in FKM. But the counterpart to this geometric flexibility is that the basic flavor of the definition is least familiar to analytic number theorists. (Here, I am reminded of Cyrano de Bergerac who, having described six different ways of going to the moon, and being asked “Which one did you choose”, replied “A seventh”; or, in proper subjunctive French, –Mais voilà six moyens excellents !. . .Quel système Choisîtes-vous des six, Monsieur ? — Un septième !)
Here the basic object is an  -adic étale sheaf on the affine line over
-adic étale sheaf on the affine line over 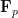 , with an added “regularity” property. It is a consequence of basic properties of such objects that, for any
, with an added “regularity” property. It is a consequence of basic properties of such objects that, for any 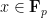 , we can look at the “stalk” at
, we can look at the “stalk” at  , which is a finite-dimensional
, which is a finite-dimensional 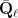 -vector space
-vector space  , and that the Frobenius automorphism (in some incarnation) acts on this vector space, allowing us to define a trace function
, and that the Frobenius automorphism (in some incarnation) acts on this vector space, allowing us to define a trace function
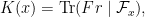
and this is how we get our trace weights from this point of view.
To get a feeling for the actual meaning of this, I would like first to refer to my old expository text on Deligne’s first proof of the Riemann Hypothesis over finite fields, where the first part is an introduction to étale cohomology, which might be useful for readers with some basic background in elliptic curves over finite fields, but who haven’t studied the étale topology yet. But here is a more down-to-earth way of seeing things, which mixes fish and fowl to some extent.
A middle-extension sheaf 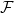 on the affine line over
on the affine line over 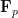 , whatever is the actual definition, comes concretely with some data. One of them is a finite set
, whatever is the actual definition, comes concretely with some data. One of them is a finite set  of singularities, which is defined over
of singularities, which is defined over 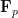 (in other words, it is the zero set of some non-zero polynomial in
(in other words, it is the zero set of some non-zero polynomial in ![\mathbf{F}_p[T] \mathbf{F}_p[T]](https://s0.wp.com/latex.php?latex=%5Cmathbf%7BF%7D_p%5BT%5D&bg=ffffff&fg=000000&s=0) ). On the complement
). On the complement 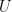 of this set, the sheaf is what is called lisse, which is equivalent to saying that there is a representation of the étale fundamental group
of this set, the sheaf is what is called lisse, which is equivalent to saying that there is a representation of the étale fundamental group 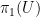 of
of 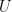 in some finite-dimensional
in some finite-dimensional 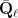 -vector space which is “equivalent” to the restriction of the sheaf to
-vector space which is “equivalent” to the restriction of the sheaf to 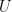 . But this étale fundamental group is, in fact, none other (canonically isomorphic) than the Galois group
. But this étale fundamental group is, in fact, none other (canonically isomorphic) than the Galois group 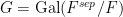 of the previous description. And in fact, if we view the representation corresponding to
of the previous description. And in fact, if we view the representation corresponding to 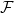 as a representation of
as a representation of 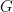 , the trace functions are the same.
, the trace functions are the same.
This allows us at least to describe how one can define the complexity of a middle-extension sheaf: one just takes the complexity of the associated Galois representation (the dimension of the vector space, plus the Artin conductor.)
What is the point then of thinking in terms of sheaves? To my mind, here are some important advantages:
- The geometric picture that arises is often the easiest way to “see” how to manipulate trace functions to construct new ones;
- There are different ways of extending a lisse sheaf on
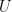 to a sheaf on the affine line, and the “middle-extension” is just one of them. It is, in some sense, the best one, but there are others. In the general theory, these may come out because some construction goes outside of the realm of middle-extension sheaves: for instance, the tensor product of two middle-extension sheaves is not one in general; this accounts in a precise way for the way the product of two trace functions may not be one exactly;
to a sheaf on the affine line, and the “middle-extension” is just one of them. It is, in some sense, the best one, but there are others. In the general theory, these may come out because some construction goes outside of the realm of middle-extension sheaves: for instance, the tensor product of two middle-extension sheaves is not one in general; this accounts in a precise way for the way the product of two trace functions may not be one exactly;
- The theory of sheaves extends handily to higher-dimensional varieties, where more types of singularities and other behaviors arise because there is “more room” for the dimension of various sets where different behaviors arise (so sheaves on a surface might be supported on a curve, etc). Here it is important to see middle-extension sheaves as just some of the étale sheaves, and to allow more general ones.
- The formalism is by far the most powerful. Especially crucial to the proofs of the deepest results (including the Riemann Hypothesis) is the existence of the étale cohomology groups of a sheaf, and of so-called “higher-direct images” (with compact support or not), which make sense for étale sheaves, but in general do not preserve such regularity properties as being lisse or middle-extension.
- As a consequence of the above, this is the language in which the sources concerning the properties of étale sheaves are written; for FKM, this means especially the books of N. Katz, which we have consulted and referenced extensively…
To conclude this first post, here is a concrete illustration of what the sheaf formalism gives that is important to analytic number theorists, and which is completely mysterious (as far as I know, at least) on the level of Galois representations or automorphic forms: the existence of the Fourier transform. In fact, given a trace weight 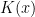 associated to some sheaf
associated to some sheaf 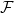 , a construction of Deligne delivers another sheaf
, a construction of Deligne delivers another sheaf  , which is still a middle-extension sheaf, and is such that the associated trace function is
, which is still a middle-extension sheaf, and is such that the associated trace function is

This construction is not obvious; in fact, it involves (1) the fact that sheaves make sense on higher-dimensional varieties, with a wide variety of “functorial” properties; (2) the fact that higher-direct images exist: this is what is needed to obtain results of the type “a sum over  of some trace functions parametrized by
of some trace functions parametrized by  is itself a trace function”…
is itself a trace function”…
If we assume the existence of this construction (and most analytic number theorists would argue that, whatever a theory of functions of algebraic origin might do, it should be compatible with Fourier transform…) we immediately expand our range of examples with some highly-interesting ones, starting with the basic cases

whose Fourier transforms are extremely interesting: they are values of families of exponential sums in one variable.
For instance, take

where we denote by  the inverse of
the inverse of  modulo
modulo  . Then we find that
. Then we find that

is a trace weight! In other words, the family of Kloosterman sums  , as a function of
, as a function of  , is a function of algebraic origin modulo
, is a function of algebraic origin modulo  …
…
Trailer! In the next posts! I will probably next describe many examples of trace functions, and discuss the formalism that allows us to manipulate them conveniently. After this, I will come to their analytic properties, where the key point is the Riemann Hypothesis over finite fields…
of finite size, it is a tautology that the column vectors of
are orthonormal, and in particular that
, if
is a separable Hilbert space: given any orthonormal basis
of
, we can define the “matrix”
representing
by
, for distinct indices
, are orthogonal in the
-sense: we have
.
is some
space, say
, and
is an integral operator on
given by a kernel
, so that
of the kernel form a kind of “continuous matrix” representing
. The question is: are its columns orthogonal? In other words, given
in
, do we have
which both define a unitary operator, and are such that the integrals
, and its kernel is
were square integrable on
, for instance, the corresponding integral operator on
would be compact, and its spectrum could not be contained in the unit circle (excluding the degenerate case of a finite-dimensional
-space.)
, and as in the previous post, we look at the unitary operator
is the principal series representation with eigenvalue
of
. The result of Cogdell and Piatetski-Shapiro already mentioned there shows that
is, indeed, a unitary operator given by a smooth kernel
for some function
on
. This function is explicit, and (as expected) not very integrable: we have
for
, this function is neither integrable nor square-integrable. But, the function
on
decays exponentially at infinity! This means that the integrals
, which are given by
and
have opposite sign (this requires also knowing that there is no problem at
, but that is indeed the case, because the Bessel functions here have just a logarithmic singularity there, and the factors
eliminate the
in the integral.)
. This boils down to an identity for integrals of Bessel functions that can be found in (combinations of) standard tables, or it can be proved more conceptually by viewing
for the function
which is the normalized characteristic function of the interval of radius
around
, and similarly for
. Since
is small enough, the unitarity gives
, which is made relatively easy by the exponential decay of
at infinity…
, is antisymmetric: we have
appearing in the Voronoi formula for the divisor function is given by
if
, but
if
. This affects the final formula: we have
instead of
, so there is no contradiction between the informal argument and the rigorous one.)