In my paper with É. Fouvry and Ph. Michel where we find upper bounds for the number of certain sheaves on the affine line over a finite field with bounded ramification, the combinatorial part of the argument involves spherical codes and the method of Kabatjanski and Levenshtein, and turns out to depend on the rather recondite question of knowing a lower bound on the size of the largest zero 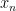 of the
of the  -th Hermite polynomial
-th Hermite polynomial  , which is defined for integers
, which is defined for integers 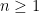 by
by
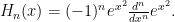
This is a classical orthogonal polynomial (which implies in particular that all zeros of  are real and simple). The standard reference for such questions seems to still be Szegö’s book, in which one can read the following rather remarkable asymptotic formula:
are real and simple). The standard reference for such questions seems to still be Szegö’s book, in which one can read the following rather remarkable asymptotic formula:
![x_n=\sqrt{2n}-\frac{i_1}{\sqrt[3]{6}}\frac{1}{(2n)^{1/6}}+o(n^{-1/6}) x_n=\sqrt{2n}-\frac{i_1}{\sqrt[3]{6}}\frac{1}{(2n)^{1/6}}+o(n^{-1/6})](https://s0.wp.com/latex.php?latex=x_n%3D%5Csqrt%7B2n%7D-%5Cfrac%7Bi_1%7D%7B%5Csqrt%5B3%5D%7B6%7D%7D%5Cfrac%7B1%7D%7B%282n%29%5E%7B1%2F6%7D%7D%2Bo%28n%5E%7B-1%2F6%7D%29&bg=ffffff&fg=000000&s=0)
where 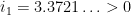 is the first (real) zero of the function
is the first (real) zero of the function
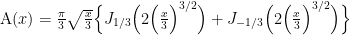
which is a close cousin of the Airy function (see formula (6.32.8) in Szegö’s book, noting that he observes the Peano paragraphing rule, according to which section 6.32 comes before 6.4).
(Incidentally, if — like me — you tend to trust any random PDF you download to check a formula like that, you might end up with a version containing a typo: the cube root of  is, in some printings, replaced by a square root…)
is, in some printings, replaced by a square root…)
Szegö references work of a number of people (Zernike, Hahn. Korous, Bottema, Van Veen and Spencer), and sketches a proof based on ideas of Sturm on comparison of solutions of two differential equations.
As it happens, it is better for our purposes to have explicit inequalities, and there is an elementary proof of the estimate

which is only asymptotically weaker by a factor 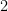 from the previous formula. This is also explained by Szegö, and since the argument is rather cute and short, I will give a sketch of it.
from the previous formula. This is also explained by Szegö, and since the argument is rather cute and short, I will give a sketch of it.
Besides the fact that the zeros of  are real and simple, we will use the easy facts that
are real and simple, we will use the easy facts that  , and that
, and that  is an even function for
is an even function for  even, and an odd function for
even, and an odd function for  odd, and most importantly (since all other properties are rather generic!) that they satisfy the differential equation
odd, and most importantly (since all other properties are rather generic!) that they satisfy the differential equation
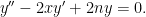
The crucial lemma is the following result of Laguerre:
Let ![P\in \mathbf{C}[X] P\in \mathbf{C}[X]](https://s0.wp.com/latex.php?latex=P%5Cin+%5Cmathbf%7BC%7D%5BX%5D&bg=ffffff&fg=000000&s=0) be a polynomial of degree
be a polynomial of degree 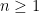 . Let
. Let 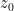 be a simple zero of
be a simple zero of 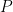 , and let
, and let
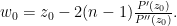
Then if 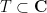 is any line or circle passing through
is any line or circle passing through 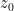 and
and 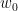 , either all zeros of
, either all zeros of 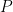 are in
are in  , or both components of
, or both components of 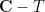 contain at least one zero of
contain at least one zero of 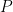 .
.
Before explaining the proof of this, let’s see how it gives the desired lower bound on the largest zero 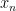 of
of  . We apply Laguerre’s result with
. We apply Laguerre’s result with  and
and  . Using the differential equation, we obtain
. Using the differential equation, we obtain
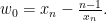
Now consider the circle  such that the segment
such that the segment ![[w_0,z_0] [w_0,z_0]](https://s0.wp.com/latex.php?latex=%5Bw_0%2Cz_0%5D&bg=ffffff&fg=000000&s=0) is a diameter of
is a diameter of  .
.

Now note that 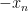 is the smallest zero of
is the smallest zero of  (as we observed above,
(as we observed above,  is either odd or even). We can not have
is either odd or even). We can not have 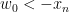 : if that were the case, the unbounded component of the complement of the circle
: if that were the case, the unbounded component of the complement of the circle  would not contain any zero, and neither would
would not contain any zero, and neither would  contain all zeros (since
contain all zeros (since  ), contradicting the conclusion of Laguerre's Lemma. Hence we get
), contradicting the conclusion of Laguerre's Lemma. Hence we get 
and this implies

as claimed. (Note that if  , one deduces easily that the inequality is strict, but there is equality for
, one deduces easily that the inequality is strict, but there is equality for 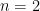 .)
.)
Now for the proof of the Lemma. One defines a polynomial 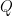 by
by

so that 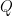 has degree
has degree 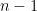 and has zero set
and has zero set  formed of the zeros of
formed of the zeros of 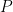 different from
different from 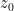 (since the latter is assumed to be simple). Using the definition, we have
(since the latter is assumed to be simple). Using the definition, we have

We now compute the value at 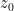 of the logarithmic derivative of
of the logarithmic derivative of 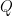 , which is well-defined: we have
, which is well-defined: we have

hence

which becomes, by the above formulas and the definition of 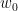 , the identity
, the identity
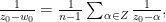
or equivalently
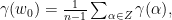
where  is a Möbius transformation.
is a Möbius transformation.
Recalling that 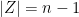 , this means that
, this means that 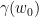 is the average of the
is the average of the  . It is then elementary that for line
. It is then elementary that for line 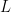 , either
, either  is contained in
is contained in 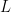 , or
, or  intersects both components of the complement of
intersects both components of the complement of 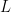 . Now apply
. Now apply 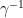 to this assertion: one gets that either
to this assertion: one gets that either  is contained in
is contained in  , or
, or  intersects both components of the complement of
intersects both components of the complement of  . We are now done, after observing that the lines passing through
. We are now done, after observing that the lines passing through 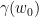 are precisely the images under
are precisely the images under 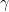 of the circles and lines passing through
of the circles and lines passing through 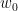 and through
and through 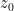 (because
(because 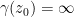 , and each line passes through
, and each line passes through  in the projective line.)
in the projective line.)

