Addendum – E. Kowalski's blog

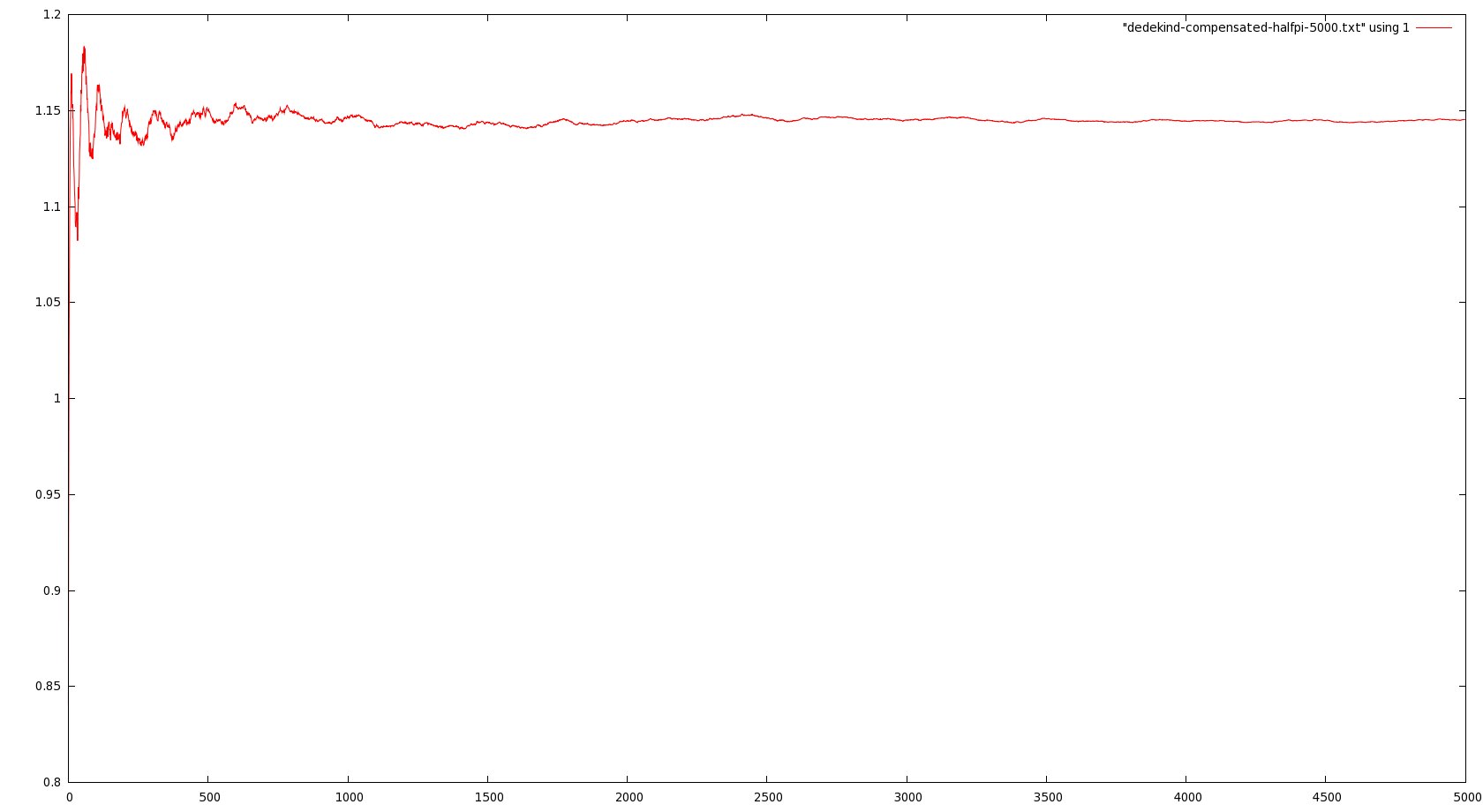
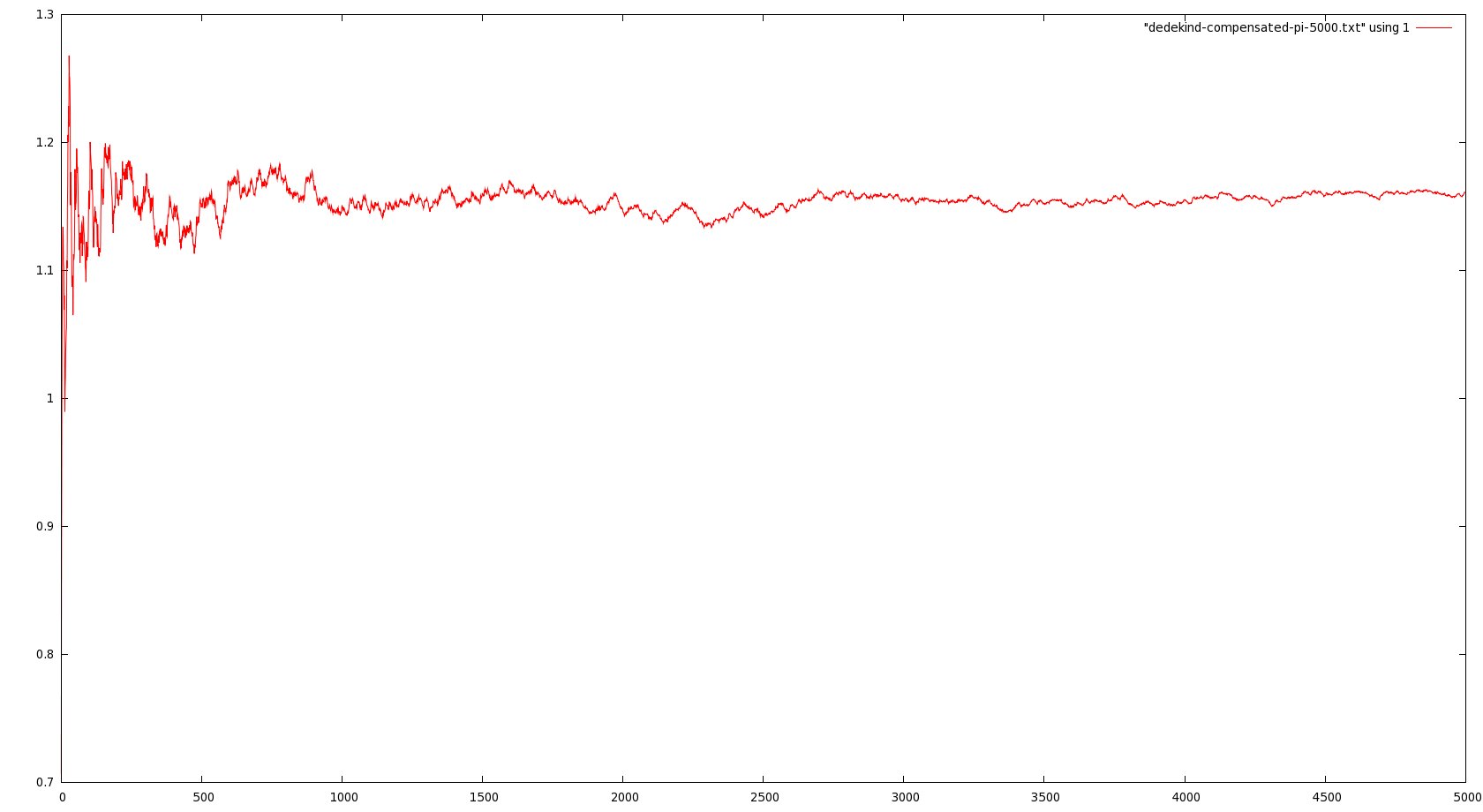
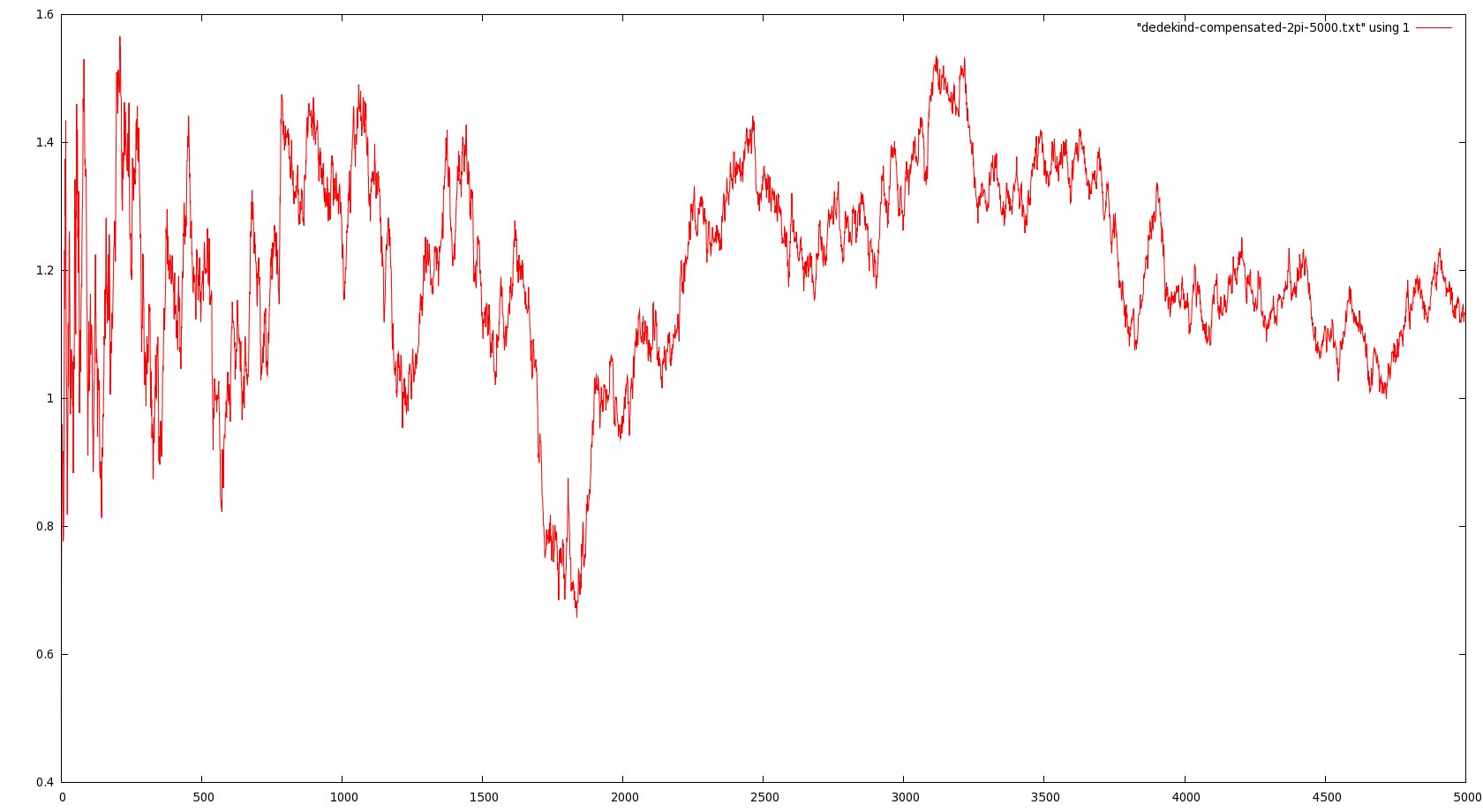
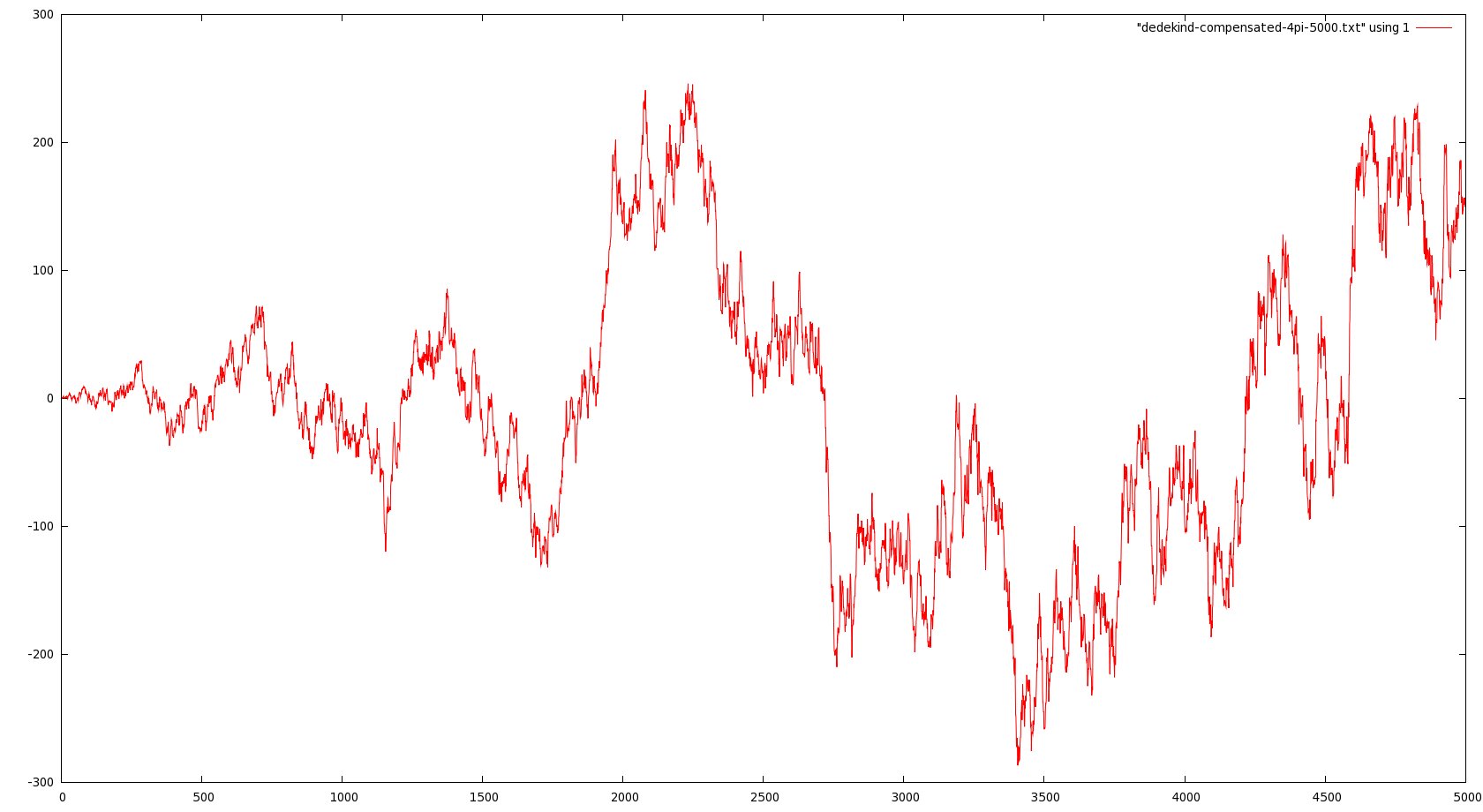
Here is a quick update to the last post about (restricted) mod-Cauchy convergence; I’ve investigated numerically the behavior of the renormalized averages

$\mathbf{E}_N(e^{its(d,c)}) \times \exp(\gamma_N |t|)$

(see the post for the notation) for some values of t, to see if the limitation to

$|t|<2\pi$

in Vardi’s result could be a mere artifact of the method. Here are some graphs representing these empirical averages for

$N\leq 5000$

(click to see the full pictures):

$t=\frac{\pi}{2}$

$t=\pi$

$t=2\pi$

$t=4\pi$

In particular, note that in the last picture, the vertical scale runs from -300 to 300, more or less, compared with oscillations between 0.5 and 1.5 in the third. So it seems pretty convincing evidence that the limit as N goes to infinity does not exist when t is large.

(Note: the empirical average for N=5000 involves about 8,000,000 Dedekind sums).

Published by

Kowalski