The complex number obtained by taking the product of the integer two, the imaginary unit i, and the area π of a disc of radius 1 can be written — in principle — in six different ways:
However, as far as I know, only the first two are commonly used. Or, to be more precise, I use exclusively the first form (which is much more euphonious when pronounced in French), and most everyone else uses the second form, with laughable justification.
I think this is an example of the more general principle that numerals go before letters — consider the polynomial 2xy + 3xz, which you’d never write (say) x2y + xz3. The fact that i and π stand for specific numbers, instead of being variables, doesn’t stop your last four forms from looking strange.
They’re ordered least to greatest. Surely, 2 < π, and if you look in the complex plane, π < i, since, after all, i is above the real line.
Or you could simply spell them out, and order most letters to least.
2 i pi is in alphabetic order. right?
Laughable justification for 2\pi i? What’s the justification for 2 i \pi?
always put the angle before the i. don’t put the i in the middle of the angle. that’s ludicrous!
I find infinitely more natural than
infinitely more natural than  . On the other hand, when
. On the other hand, when 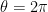 …
…
Actually I use quite a lot the third form in my first few classes introducing complex numbers in high school, to stick with the notation
in my first few classes introducing complex numbers in high school, to stick with the notation  . Swapping too early can be very confusing for the pupils.
. Swapping too early can be very confusing for the pupils.
For a francophone \pi i 2 is hideous.
P.S. Slightly off-topic:
I watched Clint Eastwood’s film “Gran Torino” yesterday.
The two main characters are named Kowalski and Tao.
What’s going on between Hollywood, ETH and UCLA?
2 is an integer, Pi is real, i is complex.
I feel that is the best way to order things.
I think that the order 2*pi*i as with expressions like 2*i*(sheaf Z) are just an instance of head-final word order of a noun phrase in english. The fact that i (or sheaf Z) comes last is because these objects are what the compound thing is (a complex number or sheaf) and thus consitute the head of the expression. Similar reasoning gives that the nested expression 2*pi has pi last.
In italian “duepigrecoì” sounds definitely better.
2i\pi is one key-button less. You do not need a space between \pi and i when writing Latex. Simply most practical:-)