Analytic Number Theory, as a discipline, is one of the natural habitat of a wonderful mathematical beast, the workaround. This can be seen, for instance, from the fact that many of the most natural consequences of the Riemann Hypothesis (and even of the Generalized Riemann Hypothesis) are known to be true unconditionally, and some have been for quite a while.
For instance, Hoheisel managed to prove (in 1930) the existence of a prime in any interval of the type N<n<N+Nθ, N large enough, for some fixed θ<1, an impressive result if one knows that the “obvious” way to prove this would be to use the (unproved!) fact that the Riemann zeta function ζ(s) has no zero with real part larger than θ. His trick was to combine known (but weak) zero-free regions for zeros of the zeta function with density theorems, which state that zeros off the critical line, if they exist, are rarer and rarer close to the line Re(s)=1. In other words, a good enough bound (tending to infinity with respect to some variable) for the cardinality of the empty set is essential.
There are many other examples but I want to discuss one today which is of much less import, though (to my mind) quite cute. It allows me to start by mentioning the Sato-Tate Conjecture. This has been proved recently in many cases for elliptic curves by R. Taylor, building on works of himself, Clozel, Harris and Shepherd-Barron; clearly I can not do better here than refer to the brilliant discussion of the statement, its meaning, and the context of the proof that can be found in Barry Mazur’s recent survey paper in the Bulletin of the AMS. I will only recall, for my purposes, that the essence of the conjecture is that, for certain very special sequences of Fourier coefficents of cusp forms, λ(p), which are indexed by prime numbers p, and all lie between -2 and 2 (in the usual analytic normalization which is criminal by algebraist’s standards…), we expect to be able to guess accurately what proportion of them (among all primes) lie in an interval α< x<β with fixed α and β. In particular, this proportion should be positive.
Now the question I want to consider is a variant of the following fairly classical one: suppose we have two sequences λ1(p) and λ2(p), coming from two different cusp forms (two distinct elliptic curves for instance, non-isogenous to be technically accurate). The sequences are known to differ; how large (in terms of the parameters, which are typically two positive integers, the weight and the conductor, though the weight is always 2 for elliptic curves) is the first prime which shows that this is the case?
There have been quite a few works on this problem, which is seen as an analogue of an even older problem of analytic number theory, that of the least quadratic non-residue modulo a prime number, where the two sequences are replaced by that of values of the Legendre symbol of p modulo another fixed prime q, whereas the other is the constant sequence 1. This earlier problem is of considerable importance in algorithmic number theory, and both have been excellent testing and breeding grounds for various important techniques, notably (and this is close to my heart…) leading to the invention and development of the first “large sieve” method by Linnik.
But I said I was interested in a variant; this is motivated by recent work of Lau and Wu, exploring the structure of the set of sequences sharing the same first few terms. For the quadratic non-residue problem, they have essentially found an optimal “threshold” y for which they know quite precisely how many sequences coincide for primes up to y (the number is in terms of the conductor, this being the only parameter left). They have a similar upper bound for the case of cusp forms, but it is unlikely to be sharp, for the simple reason that the coefficients λ(p) may take many more than the two values -1 and 1 (and sometimes 0) taken by Legendre symbols, so that repeated coincidences should occur much more rarely.
And this leads, at last, to the question of interest here: suppose, instead of looking at the values of the Fourier coefficients, we only retain their signs? Because they are real (at least in many cases of interest), this eliminates the difference between the number of values. (We may either take the sign of 0 to be 0, or we may, to make the problem harder, consider that 0 is compatible with both signs).
Before we can try to see if the Lau-Wu threshold is likely to be correct, there is an even simpler question that must be answered first, and that has at least a naive appeal: given two sequences λ1(p) and λ2(p) as above, assume now that their signs coincide (or are compatible if we want to have 0 be of both signs) for all primes p. Are the sequences identical? What about if we allow for the signs to coincide except for a small proportion of the primes?
What is the link with the Sato-Tate Conjecture? Well, one of the standard ways to detect that two modular forms are in fact the same is to use one of the famous corollaries of the Rankin-Selberg method: summing the product λ1(p)λ2(p) over primes p<X leads to a quantity S(X) which is either bounded as X grows, or behaves like π(X) (the number of primes up to X), depending on whether the sequences are distinct or the same. This dichotomy implies that, if we can show that the sum S(X) grows (however slowly!) as X gets large, the first alternative being wrong, we must indeed have started with identical sequences.
The point is that if the signs of the two sequences are compatible, the product λ1(p)λ2(p) is always non-negative. This does not by itself imply that S(X) grows unboundedly: it could be that the absolute value of the two sequences are always balancing so that the product is small enough to define an absolutely convergent series.
But the Sato-Tate law at least immediately implies that for each sequence independently, there is a positive proportion of primes where |λ1(p)|> α for any fixed α>0. If we take α small enough, the proportion will be >1/2, so there will be a (smaller) positive proportion of primes where both sequences are “large” in absolute value. Since S(X) is (by positivity) at least as large as any partial sum, we win.
Now, for the workaround… The Sato-Tate law is only a theorem for a restricted class of modular forms. For non-holomorphic cusp forms in particular, it seems very hard to prove. Can we still show that the sequence of signs of their Fourier coefficients determines uniquely such modular forms? Yes, by adapting slightly an idea of Serre that he used to show that various other consequences of the Sato-Tate Conjecture could be derived from the accumulated known results concerning the existence of symmetric power L-functions (which, since the irruption of the Langlands program, seem to be the most natural way to attack this type of conjectures).
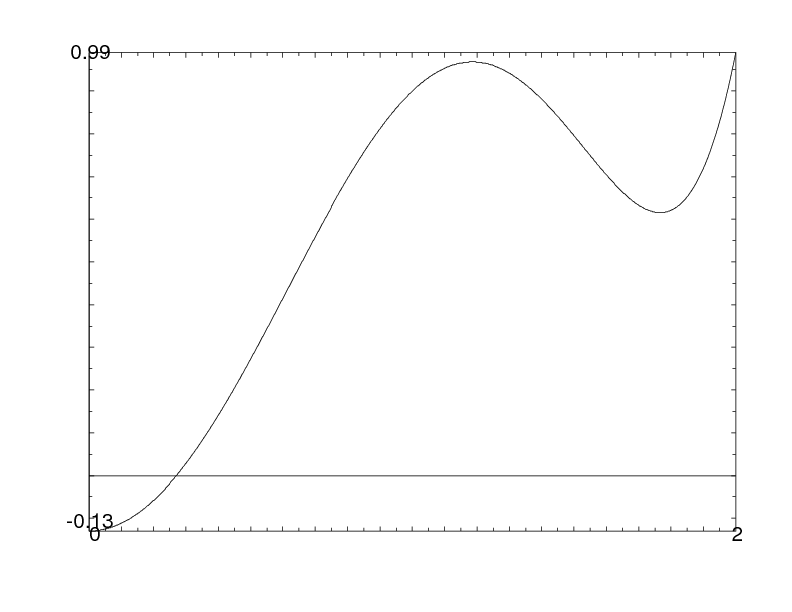
Here the idea is to find some even real polynomial P of small degree (4 if using symmetric fourth powers, 6 if using symmetric sixth powers, and so on) with graph looking like this (for non-negative values):
The idea is that the sum of P(λi(p)) over p<X is clearly smaller than the sum of the coefficients over primes where λi(p)>α, where α is the real zero of P that we see on the picture. On the other hand, by decomposition P as a sum of Chebychev polynomials X2j, j even (which, evaluated at the Fourier coefficients, represent the coefficients of the 2j-th symmetric power), the sum is asymptotically the same as a0π(X), where a0 is the coefficient of X0=1, if we know that the polynomial only involves symmetric powers for which we know there is no pole at s=1. If moreover this leading coefficient is >1/2, it follows that the set of primes where the Fourier coefficients in both sequences are simultaneously >α has positive density, and one can conclude as we did under the Sato-Tate Conjecture.
So can we implement this? With 6th powers, we can, but not with 4th powers only! Indeed, one can easily show that there is no polynomial P=a0X0+a2X2+a4X4 such that P(0)≤0, a0>1/2, and P≤1 on [0,2]. But the polynomial P=X2-X4/4 is “borderline”: it only fails because a0=1/2 in this case. Then we can simply add small multiples of X0 and X6 to obtain the graph above, the 6th-power being adjusted to compensate for the increase of a0 above 1/2.
The simplicity of the argument shouldn’t obscure the depth of the underlying tools: the analytic continuation and absence of pole at s=1 of the 4th and 6th symmetric powers is a very recent fact, proved by Kim and Shahidi in 2002.
(To conclude, I should say that it’s very possible that this question has already been considered, although looking in Math. Reviews didn’t turn out any directly related paper; I’d be happy to mention any earlier work, of course; also I’ve disregarded some issues, e.g., having to do with CM forms. For details of the arguments and a few other questions, see this short note).