After a small break while traveling, I continue the discussion of my paper with Fouvry and Michel, continuing from here. But first of all, I’m happy to mention two proofs of the counting identities mentioned in my introductory post: one that D. Zywina has sent me, a nice proof based on explicit computations of modular forms and functions, and another that is in fact just an application of a more general result of Deligne and Flicker on local systems on the projective line minus four points (see Section 7 of this preprint).
Now, if memory serves, at the end of the last post, we saw that analytic techniques reduce the study of our sums
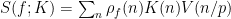
to the study of correlation sums

where  is the normalized Fourier transform modulo
is the normalized Fourier transform modulo  .
.
For these, we need to show that “most” are small in order to conclude. Fixing a parameter 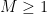 , let us therefore define
, let us therefore define 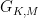 to be the set of matrices
to be the set of matrices 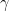 in
in 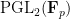 such that
such that
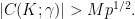
The discussion in the previous post shows that if, for some 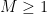 , all matrices in
, all matrices in 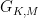 are upper-triangular, we get
are upper-triangular, we get
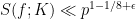
for any 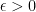 . But we can deal with some more exceptions. More precisely, we show that this estimate is still valid, with an implied constant depending only on
. But we can deal with some more exceptions. More precisely, we show that this estimate is still valid, with an implied constant depending only on 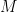 , if the matrices in
, if the matrices in 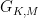 are all either
are all either
- parabolic (they have a single fixed point in
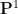 ), or
), or
- upper-triangular, or
- if they either fix or permute two distinct points taken in a finite list, say containing at most
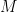 pairs
pairs 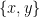 .
.
Compared with the previous discussion, the subtlety here is that it can indeed happen that such matrices appear in the transformations we apply to 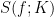 , and proving that their contributions remain under control involves some rather fun analysis.
, and proving that their contributions remain under control involves some rather fun analysis.
This summarizes, in a rather hurried fashion, the first part of our paper. Logically, we obtain statements which are self-contained, but which are only applicable directly in a few cases (the case  is an excellent example where this can be done). To go further, we need to use algebro-geometric tools.
is an excellent example where this can be done). To go further, we need to use algebro-geometric tools.
And here comes a dilemma well-known to anyone who has had to present research involving two relatively distant areas of mathematics, so that specialists of one may not know the other. I can give a concise definition of the class of weights 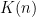 that we consider, and it will be immediately familiar and natural to algebraic geometers — but not to most analytic number theorists.
that we consider, and it will be immediately familiar and natural to algebraic geometers — but not to most analytic number theorists.
So, instead, I will just say (very fast) that these weights, which we call “irreducible trace weights”, are trace functions of geometrically irreducible  -adic middle-extension Fourier sheaves pointwise pure of weight
-adic middle-extension Fourier sheaves pointwise pure of weight 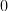 on
on  . Then I will defer to a later post a more leisurely run-through this definition, together with more examples of weights and their formalisms, and with some further analytic properties which are of independent interest.
. Then I will defer to a later post a more leisurely run-through this definition, together with more examples of weights and their formalisms, and with some further analytic properties which are of independent interest.
The reason this class of weight “works” can however be quickly summarized in a rather miraculous property, which is essentially a consequence of the Riemann Hypothesis: assuming 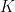 has small complexity (in a precise sense, saying basically that it comes from a sheaf with small rank and small ramification), the correlation sum
has small complexity (in a precise sense, saying basically that it comes from a sheaf with small rank and small ramification), the correlation sum  is either
is either 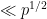 , where the implied constant depends only on the numerical invariant measuring the complexity of the weight, or we have an equality
, where the implied constant depends only on the numerical invariant measuring the complexity of the weight, or we have an equality
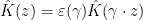
for all  and some fixed complex number
and some fixed complex number 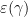 of modulus
of modulus 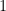 . From this second part, we see that, for a suitable
. From this second part, we see that, for a suitable 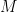 , the set
, the set 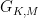 discussed above is contained in the group
discussed above is contained in the group 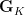 of all
of all 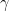 (viewed in
(viewed in 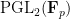 ) for which there exists
) for which there exists 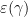 (of modulus
(of modulus 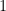 ) such that the identity above holds. This provides us with enough structure on the set of “bad” matrices (with large correlation sums), from which the bound
) such that the identity above holds. This provides us with enough structure on the set of “bad” matrices (with large correlation sums), from which the bound
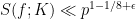
can fairly simply be deduced for irreducible trace weights using the automorphic part of our paper.
Indeed, we distinguish two cases, depending on the structure of the subgroup 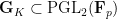 :
:
- If
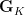 has order coprime to
has order coprime to  , we use the classification of such subgroups, and see that
, we use the classification of such subgroups, and see that 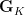 is either contained in the normalizer of some maximal torus, i.e., in the stabilizer of a two-point set
is either contained in the normalizer of some maximal torus, i.e., in the stabilizer of a two-point set 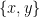 (and hence these weights fall under the third case (3) of allowed “bad” matrices) or otherwise
(and hence these weights fall under the third case (3) of allowed “bad” matrices) or otherwise 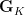 is of order at most
is of order at most 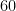 , and consists only of semisimple elements (which allows us again to apply (3), with possibly more than one pair
, and consists only of semisimple elements (which allows us again to apply (3), with possibly more than one pair 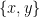 involved, but less than
involved, but less than 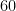 );
);
- If
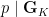 , we find some element
, we find some element  in
in 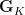 which is of order
which is of order  , hence unipotent. Thus
, hence unipotent. Thus  acts transitively on
acts transitively on 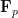 (minus at most a single point); the formula defining the subgroup
(minus at most a single point); the formula defining the subgroup 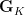 above implies easily that
above implies easily that  is then basically of a very restricted type, namely
is then basically of a very restricted type, namely
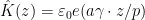
for some fixed matrix 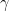 and fixed complex number
and fixed complex number  and integer
and integer  . But this weight comes from a specific (Fourier transform of a) Artin-Schreier sheaf (it might not be the one defining
. But this weight comes from a specific (Fourier transform of a) Artin-Schreier sheaf (it might not be the one defining 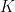 originally, but a fortiori, we can assume it is!). For this sheaf, a rather simple analysis shows that
originally, but a fortiori, we can assume it is!). For this sheaf, a rather simple analysis shows that 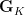 is a unipotent group isomorphic to
is a unipotent group isomorphic to 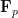 (unless
(unless 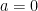 or
or 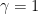 , which are exceptional cases). So the bad matrices are either trivial or parabolic, and we can appeal to case (1) to handle these weights…
, which are exceptional cases). So the bad matrices are either trivial or parabolic, and we can appeal to case (1) to handle these weights…
I will conclude for today with another fact we noticed only very recently: in the special case 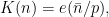 it turns out that the correlation sums had already appeared in a paper of Friedlander and Iwaniec on incomplete Kloosterman sums, in the special case of
it turns out that the correlation sums had already appeared in a paper of Friedlander and Iwaniec on incomplete Kloosterman sums, in the special case of  when
when 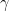 is lower-triangular (and non-diagonal). In the Appendix to this paper, Birch and Bombieri give two proofs of the estimate
is lower-triangular (and non-diagonal). In the Appendix to this paper, Birch and Bombieri give two proofs of the estimate  (for lower-triangular matrices): one is geometric (based on counting points on surfaces over finite fields), but the second one has amusing links to our arguments, with a camouflaged sighting of the group structure of the group
(for lower-triangular matrices): one is geometric (based on counting points on surfaces over finite fields), but the second one has amusing links to our arguments, with a camouflaged sighting of the group structure of the group 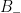 of lower-triangular matrices and of the fact that
of lower-triangular matrices and of the fact that 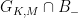 is contained in a subgroup of
is contained in a subgroup of 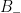 … (Interestingly, there is no trace of modular forms in this paper of Friedlander and Iwaniec, so the coincidence is rather unexpected.)
… (Interestingly, there is no trace of modular forms in this paper of Friedlander and Iwaniec, so the coincidence is rather unexpected.)