Thanks to the recent conference celebrating the 25th anniversary of the Zahlentheorie Seminar, and even more as this week’s conference for Fouvry’s 60th Birthday in Marseille, I have been able to talk with a number of people about Zhang’s result on bounded gaps between primes, especially Philippe Michel, Paul Nelson and Étienne Fouvry. All generic “our”s and “we”s below refer to these discussions.
We have concentrated exclusively on the critical “ternary-divisor” part of the argument, and attempted many variants and reconfigurations. Our goal is not really to do better than Zhang (in terms of exponents), but to see by direct experience what works and what doesn’t.
Quite a few of these attacks failed, which of course helps in building some understanding. But two or three directions are promising, and one definitely does seem to lead to a different version of the argument. We have not yet written full details, but the approach succeeds (i.e., it definitely breaks the barrier of the Riemann Hypothesis, which is the whole game) in getting an exponent of distribution
for the ternary divisor function with nicely factorable moduli, at a level of informality which inspires great confidence. (When applied in the context of my previous papers with Fouvry and Michel, this type of sketches give fully consistent exponents and uniformity in comparison with the final papers.)
Here are just some remarks. We view the basic problem as understanding
where is the squarefree modulus, which should therefore (to beat RH) be of size a bit larger than
(by a small positive power of
), and
is fixed (though one can try to exploit average over it, and it will be important in the end that it be relatively small). In fact, quite a few attempts purposely express this as a special case of
for some general “trace function” (these are more general than usually discussed, both because the modulus is not prime, and because the -normalized characteristic function of a residue class modulo a prime is only the trace function of a perverse sheaf, and not a standard lisse sheaf, but that last point is not particularly problematic). The idea is that we want to exploit the general context and insights that we have developped about these objects.
In contrast to what I mentioned in my last post, it does seem that the factorization of moduli in the ternary case is crucial, but the cancellation from Ramanujan sums might not be (although of course extra cancellation can not hurt…)
On the other hand, in trying to work with a generalish , we understand now this extra cancellation at a higher level: it is not a super-specific fact about Ramanujan sums, but the latter is a concrete illustration of a fundamental phenomenon concerning trace functions of the so-called (pointwise pure) “middle-extension” sheaves, due to Deligne: at a singularity of such a sheaf, the Frobenius eigenvalues have lower weights than at “generic” points (see Lemma 1.8.1 in Weil II), and often strictly lower. (On the automorphic side, it corresponds to the well-known fact that the Satake parameters at a ramified prime are smaller in absolute value than the Ramanujan-Petersson bound at the unramified primes.)
In this picture, the Ramanujan sums correspond to the singularity at of the basic Kloosterman sheaf. (Of course one doesn’t need Deligne to estimate Ramanujan sums, but we can now confidently play complicated games with the trace functions without being afraid of having lost a very special property of these particular sums…)
The working technique also shows that one can argue without the Weyl-type shifts in the original paper — this was not entirely surprising since Heath-Brown’s improvement of the Friedlander-Iwaniec exponent for the bare (and also ours) do not involve such shifts.
Finally, all our current attempts to play games to avoid Deligne-level estimates for exponential sums have hit barriers…
There is of course still much to be done.
I like the remark concerning Satake parameters at ramified primes, because it’s something I understand. I just went back and read “Trace functions I.” Is it easy to explicitly describe the classical Kloosterman sheaf? Is it something like R^1 pi_* of a constant sheaf of an elliptic curve over (an open set) U?
The Kloosterman sheaf (of rank 2) can be constructed in two ways (at least): either as the Deligne sheaf-theoretic Fourier transform of the rank 1 sheaf [which is roughly
[which is roughly  for
for  ,
, 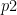 the two projections to the affine line of
the two projections to the affine line of 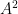 with coordinates
with coordinates 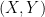 ], or as a multiplicative convolution of two rank 1 sheaves of type
], or as a multiplicative convolution of two rank 1 sheaves of type  . The second construction has the advantage of generalizing (with multiple convolutions) to higher-rank Kloosterman sums, whereas the Fourier transform of the rank 3 Kloosterman sheaf does not seem to be something “standard”.
. The second construction has the advantage of generalizing (with multiple convolutions) to higher-rank Kloosterman sums, whereas the Fourier transform of the rank 3 Kloosterman sheaf does not seem to be something “standard”.
I think the Kloosterman sheaf is not directly related to families of elliptic curves (because of wild ramification at infinity, which is rare for elliptic curves). On the automorphic side, I think the first direct construction (i.e., without applying a converse-type theorem to one of the preceeding constructions) is given by the recent (more general) work of Heinloth, Ngo and Yu.