While writing the chapters about compact groups in my notes, I had a few times the impression that it would be useful to use the fact that there is a basis of conjugacy-invariant neighborhoods of 1 in such a group. This thought would then fork in two subthreads, one in which I noticed that I didn’t really see how to prove this, and the second in which I realized I didn’t need it anyway.
This happened again during the last week-end, with the difference that I thought of trying to prove this property using representation theory. I failed at first, and finally tried to look it up online to make sure the property was actually true. Indeed, it is, and I found this book, which has three proofs (of a slightly more general statement). But I have to admit to having an inferiority complex with respect to general topology: any argument that goes on for more than a few lines without being transparent tends to make me uneasy and confuse me, and this is what happened with these arguments.
So I tried again to use representations, and indeed it works! Here’s the idea: the regular representation of
on
(with respect to Haar measure) is faithful, and gives a continuous injection
where the unitary group is given the strong operator topology (if
is infinite, it is not continuous for the operator norm topology). Hence this map is a homeomorphism onto its image (we use here the compactness of
). What we gain from seeing
in this way as a subgroup of the unitary group of a (typically) infinite-dimensional space, and with a “strange” topology to boot, is a concrete description of a basis of open neighborhoods of 1, which is open to further manipulations.
Indeed, from the definition of the strong topology on , any open neighborhood
of 1 contains a finite intersection of sets of the type
where has norm 1 and
. It is then easy to see, using unitarity, that the conjugacy-invariant subset
is equal to
where
is the orbit of under
. But the strong continuity of
implies that the orbit map
is continuous for fixed
, so that
is compact in
(as image of a compact set under a continuous map; here
has the usual norm topology).
It is then a quick application of a standard compactness argument and splitting of epsilons to check that is a neighborhood of 1 contained in
, and intersecting finitely many of these, we see that
contains indeed a conjugacy invariant neighborhood of 1…
I really can’t say that it is simpler than the purely topological argument (mostly because one needs to know about Haar measure!), but I find this rather nice as an exercise. It illustrates how representation theory can be useful to study a general compact group, at a very basic level, and also shows that it may be useful to embed (or project, with the orbit map) a compact group into complicated-looking infinite-dimensional beasts… (Of course, if has a faithful finite-dimensional representation, this can be used instead of
, but the purely topological argument becomes also much simpler.)
So, I think the pure topological neighborhood is pretty nice and doable. I don’t know if this is any better than what is in your book, but here it is…
Lemma: Let X be a topological space and let K be a compact topological space. Let U be an open subset of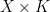 . For
. For  , write
, write 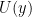 for the open subset of X such that
for the open subset of X such that  . Set
. Set  . Then V is open in X.
. Then V is open in X.
Proof: Let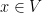 . We must show that V contains an open nbhd of x. Since
. We must show that V contains an open nbhd of x. Since 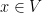 , for every
, for every  , we have
, we have 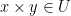 . Using that U is open, and the defn of the product topology, there are open sets
. Using that U is open, and the defn of the product topology, there are open sets  and
and 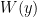 in X and K, containing x and y, such that
in X and K, containing x and y, such that  . Since K is compact, there are finitely many points
. Since K is compact, there are finitely many points 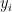 such that
such that  . Then $\bigcap V(w_i)$ is the required nbhd of x in V. QED
. Then $\bigcap V(w_i)$ is the required nbhd of x in V. QED
Application: Take , your compact group. Let Omega be any nbhd of the identity, and let
, your compact group. Let Omega be any nbhd of the identity, and let 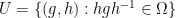 . So the lemma shows that
. So the lemma shows that  is open. This is clear conjugacy invariant, contains the identity, and is contained in
is open. This is clear conjugacy invariant, contains the identity, and is contained in 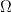 .
.
That is indeed nice and understandable! I didn’t think about introducing the product topology, but it really makes the argument clean. Thanks a lot!