I have just added to my notes on representation theory the very cute formula of Frobenius that gives, in terms of irreducible characters, the number of representations of a given element
as a commutator
in a finite group
:
where runs over the irreducible (complex) characters of
(this is Proposition 4.4.3 on page 118 of the last version of the notes).
I wanted to mention some applications, and had a vague memory that this was used to show that most or all elements in various simple groups are actual commutators. By searching around a bit, I found out easily that, indeed, there was a conjecture of Ore from 1951 to the effect that the set of commutators is equal to for any non-abelian finite simple group
, and that (after various earlier works) this has recently been proved by Liebeck, O’Brien, Shalev and Tiep.
I mentioned this of course, but then I also wanted to give some example of non-commutator, and decided to look for this using Magma (the fact that I am recovering from a dental operation played a role in inciting me to find something distracting to do). Here’s what I found out.
First, a natural place to look for interesting examples is the class of perfect groups, of course not simple. This is also easy enough to implement since Magma has a database of perfect groups of “small” order. Either by brute force enumeration of all commutators or by implementing the Frobenius formula, I got the first case of a perfect group , of order
, which contains only
distinct commutators.
Then I wanted to know “what” this group really was. Magma gave it to me as a permutation group acting on letters, with an explicit set of
generators, and with a list of
relations, which was not very enlightening. However, looking at a composition series, it emerged that
fits in an exact sequence
This was much better, since after a while it reminded me of one of my favorite types of groups: the Weyl groups of the symplectic groups
(equivalently, the “generic” Galois group for the splitting field of a palindromic rational polynomial of degree
), which fit in an relatively similar exact sequence
From there, one gets a strong suspicion that must be the commutator subgroup of
, and this was easy to check (again with Magma, though this is certainly well-known; the drop of the rank of the kernel comes from looking at the determinant in the signed-permutation
-dimensional representation, and the drop from
to
is of course from the signature.)
This identification is quite nice, obviously. In particular, it’s now possible to identify concretely which elements of are not commutators. It turns out that a single conjugacy class, of order
, is the full set of missing elements. As a signed permutation matrix, it is the conjugacy class of
and the reason it is not a commutator is that Magma tells us that all commutators in have trace in
(always in the signed-permutation representation). Thus the trace
doesn’t fit…
At least, this is the numerical reason. I feel I should be able to give a theoretical explanation of this, but I haven’t succeeded for the moment. Part of the puzzlement is that this behavior seems to be special to , the Weyl group of the root system
. Indeed, for
, the corresponding derived subgroup is not perfect, so the question does not arise (at least in the same way). And when
, the derived subgroup
of
is indeed perfect, but — experimentally! — it seems that all elements of
are then commutators.
I haven’t found references to a study of this Ore-type question for those groups, so I don’t know if these “experimental” facts are in fact known to be true. Another question seems natural: does this special fact have any observable consequence, for instance in Galois theory? I don’t see how, but readers might have better insights…
(P.S. I presume that GAP or Sage would be equally capable of making the computations described here; I used Magma mostly because I know its language better.
P.P.S And the computer also tells us that even for the group above, all elements are the product of at most two commutators, which a commenter points out is also a simple consequence of the fact that there are more than
commutators….
P.P.P.S To expand one of my own comments: the element above is a commutator in the group
itself. For instance
with
and
where .)
I hate to make such a trivial comment, but I’d like to point out that the fact that all elements are the product of two commutators follows from the fact that 120 is less than half of 960.
For any subset S of a group G larger than half the group, one has S*S = G. As an example application, every residue modulo an odd prime is the sum of two squares.
Of course! Thanks for pointing this out… It seems to be a simple fact I have trouble accepting, since someone else also reminded me of that a few months ago, in a different context. What is most amusing is that I’ve used the case of quadratic residues in number theory classes… (And my notes contain the clever variant with three subsets of Nikolov and Pyber…)
You might be interested in the discussion of this over at Mathoverflow, in particular Torsten Ekedahl’s answer http://mathoverflow.net/questions/44269/commutator-subgroup-does-not-consist-only-of-commutators/45171#45171
Thanks, it’s quite interesting. I wonder if there’s a link between the minimal examples of order 96 and the one of order 960…
I looked at the groups of order 96, and I don’t see how they could be related to the one I found.
Out of curiosity I also looked at commutators in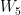 itself, and it turns out that all elements of the derived subgroup are commutators of elements in
itself, and it turns out that all elements of the derived subgroup are commutators of elements in 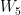 …
…
Maybe the moment has passed, but I thought it might be worth making a few comments. Obviously you are interested in finite groups above, but commutators are very important in the theory of infinite groups too. The *commutator length* of an element (of the commutator subgroup) is the least number of commutators whose product is the given element, and the *commutator width* is the supremum of this number over all elements. In the world of infinite groups, the “typical” phenomenon is that commutator width is infinite. In fact, one can define the *stable commutator length* of an element g in [G,G] to be the limit of cl(g^n)/n. In a (nonabelian) free group F (in fact, in a torsion-free hyperbolic group), the stable commutator length of *every* element of [F,F] is positive – in fact, it is at least 1/2. Stable commutator length is closely related to 2-dimensional bounded cohomology, and has many interesting connections to geometry, dynamics, etc.; see eg. http://www.its.caltech.edu/~dannyc/scl/toc.html
Thanks for the comments! I’ve already seen talks on this (including one by you…) and since I like any quantitative aspects of interesting discrete groups, I certainly hope to learn more of this one day.
It looks like group W_5 sutisfy condition (*) from paper I. M. Isaacs: Commutators and the Commutator Subgroup. The American Mathematical Monthly. Vol. 84, No. 9 (Nov., 1977), pp. 720-722 http://math.uga.edu/~pete/Isaacs77.pdf
If it is so, the fact that its commutator subgroup contains noncommutator follows from Isaacs’s theorem.