In arithmetic and geometry, there is a well-known split between right-wingers who write
and left-wingers who prefer
More insidious and mysterious is the deeper split between the inliners who write
and the redoubtable subscripters who will only write
I’ve used almost exclusively the first (almost because I don’t think a paper referring to E(8,Z) could possibly be accepted), but I have no particular memory of why I started. Does anyone have an argument (in bad faith or otherwise) for either choice?
On the first, I usually write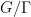 and then feel bad about it because I’m always really thinking that
and then feel bad about it because I’m always really thinking that  is acting on the left.
is acting on the left.
On the second, I always define a macro for SL, GL, etc., so I can vacillate between the two choices at random. I think I usually end up going with the second, though I have go really justification for doing so.
I tend to have a slight preference for left actions of a group G on a space X instead of right actions
of a group G on a space X instead of right actions 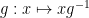 as one does not need to invert g. This of course ultimately an artefact of our arbitrary (and not completely universal) convention to put functions to the left of their arguments, rather than to the right.
as one does not need to invert g. This of course ultimately an artefact of our arbitrary (and not completely universal) convention to put functions to the left of their arguments, rather than to the right.
One slight advantage of using instead of
instead of  is that one can talk about the abstract algebraic group
is that one can talk about the abstract algebraic group  without reference to any base ring or field. I guess one could also do so with
without reference to any base ring or field. I guess one could also do so with  , of course…
, of course…
Someone writing L(f,s) for the L-function of an object f might consider as not a problem to write SL(2,Z) even for the abstract algebraic group ;)
Hence another question, why L(f,-) instead of L_f ?
I tend to use SL(2) to denote the algebraic group… (And then one can always call it G)
As far as L-functions are concerned, L(f) is the analytic function, L(f,s) is its value.
Terence, I don’t understand your point: if you want a right action, just write it as g:x—>xg. After all monoids can act on spaces on the right, no?
I prefer SL_2(), so as to emphasize the functorial nature of the group-scheme:there is just one slot, ready to devour any unsuspecting straying ring.
I prefer SL_2 for the functorial reasons expressed by others. And Gamma \ G. Do people who write G / Gamma write K \ G / Gamma?
The times I’ve seen people write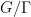 , it seems they never took a quotient on the other side by a compact subgroup… (Maybe I’m just not going to the right conferences!)
, it seems they never took a quotient on the other side by a compact subgroup… (Maybe I’m just not going to the right conferences!)
I agree with Emmanuel’s last comment. I prefer H\G since double cosets occur quite often… For instance,
SL_2(Z)\H
which is
SL_2(Z)\(SL_2(R)/SO_2(R)).
Note that (on a teaching point of view) this quotient is locally compact Hausdorff since SO_2(R) is compact, which implies that the projection map is proper.
Likewise, I don’t think I’ve ever seen anyone write K \ G / Gamma. In fact, in my experience the dividing line between those who use G/Gamma instead of Gamma\G is that the former don’t think of the symmetric space X as G/K but rather as the primary object, so that G = Isom(X) and one writes X/Gamma even though G is definitely acting on the left. This is what most low-dimensional topologists do with X = hyperbolic space; I’ve hung out with enough lattices and number theory folks that I write Gamma \ X now, as one should…
AK_47: it depends to some extent on one’s conventions, but I would not actually consider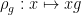 to be an action of
to be an action of 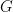 , but rather of its reversal
, but rather of its reversal  , because one has
, because one has  rather than
rather than  . Of course this is only a very minor distinction and rarely causes real difficulty in practice.
. Of course this is only a very minor distinction and rarely causes real difficulty in practice.
Terry, you’re right that it’s just words (and so not important), but the formula you don’t like literally is the meaning of “right action of G”, and it seems worthwhile to give that viewpoint a name (as opposed to putting in the opposite group). It’s like contravariant versus covariant functors: one could always introduce an “opposite category” to make everything covariant (some do this, which drives me crazy), but in various situations this creates more confusion than it’s worth since the “natural” structure (which may be simultaneously get used for other things too) really is “acting on the right” or “contravariant” (especially when a group is acting on both a space and sheaf over it at the same time), and so life is simpler by allowing the other concept (right, contravariant) to be considered on equal footing. Nathan, for writing K\G/Gamma, take a look at the end of Prop. 3.8 in Deligne’s 1968 Bourbaki expose on \ell-adic representations. :) (But in fairness, that convention has long since fallen out of favor.)
Complement: Deligne’s talk can be found here (and in case some wonder: Deligne uses a right action of SL(2,Z), and a left action of the compact subgroup, so his notation is consistent, if now unusual.)
If I remember right, the proof (at least, those I have seen) of the Skolem-Noether [or shouldn’t it be Noether-Skolem?] Theorem (any automorphism of a central simple algebra is an inner automorphism) also involve some dizzying juggling between simultaneous left and right-module structures on various rings.
In a similar vein, there are two definitions of left/right cosets (in French, classes à droite, à gauche) of a subgroup $H$ of a group $G$. I prefer to call a left coset an orbit $Hg$ of the left action of $H$ on $G$, but other people, e.g., Bourbaki, don’t agree.
I don’t think I’ve ever referred to the side of cosets explicitly, fortunately, since I would certainly not remember which convention to use (yours seems very reasonable, but Bourbaki’s opinion also carries some weight…)
I would usually say “an H-coset in G“, or something similar, which would be unambiguous in almost all situations, the action being clear from context (though it must happen sometimes that the same group, or two groups identified with the same letter, act simultaneously on the left and right, I haven’t had to worry about this yet…)