Exercise – Page 2 – E. Kowalski's blog

0.00023814967230605090687395214144185337601

Yesterday my younger son was playing dice; the game involved throwing 6 dices simultaneously, and he threw a complete set 1, 2, 3, 4, 5, 6, twice in a row!

Is that a millenial-style coincidence worth cosmic pronouncements? Actually, not that much: since the dices are indistinguishable, the probability of a single throw of this type is

$\frac{6!}{6^6}\simeq 0.015432098765432098765432098765432098765,$

so about one and a half percent. And for two, assuming independence, we get a probability

$\frac{(6!)^2}{6^{12}}\simeq 0.00023814967230605090687395214144185337601,$

or a bit more than one chance in five throusand. This is small, but not extraordinarily so.

(The dices are thrown from a cup, so the independence assumption is quite reliable here.)

Leo’s first theorem

I learnt the following from my son Léo: the teacher asks to compute $9+9$ ; that’s easy
$9\ +\ 9\ =\ 18.$
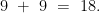
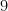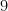But no! The actual question is to compute $9$ times $9$ ! We must correct this! But it’s just as easy without starting from scratch: we turn the “plus” cross a quarter turn on the left-hand side:
$9\ \times\ 9$
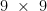
and then switch the digits on the right-hand side:
$9\ \times\ 9\ =\ 81.$

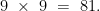
This is a fun little random fact about integers and decimal expansions, certainly.

But there’s a bit more to it than that: it is in fact independent of the choice of base 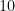$10$ , in the sense that if we pick any other integer 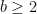$b\geq 2$ , and consider base 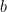$b$ expansions, then we also have

$(b-1)\ +\ (b-1)\ =\ 2b-2\ =\ b+(b-2)= \underline{1}\,\underline{b-2}$

as well as

$(b-1)\ \times\ (b-1)\ =\ (b-1)^2=b(b-2)+1= \underline{b-2}\,\underline{1},$

(where we underline individual digits in base 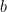$b$ expansion.)

At this point it is natural to ask if there are any other Léo-pairs 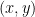$(x,y)$ to base 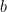$b$ , i.e., pairs of digits in base 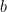$b$ such that the base 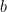$b$ expansions of the sum and the product of $x$ and $y$ are related by switching the two digits (where we always get two digits in the result by viewing a one-digit result $z$ as $\underline{0}\, \underline{z}$ ).

It turns out that, whatever the base 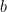$b$ , the only such pairs are 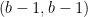$(b-1,b-1)$ and the “degenerate” case $(0,0)$ .

To see this, there are two cases: either the addition $x+y$ leads to a carry, or not.

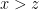If it does, this means that $y=b-z$ where $x>z$ . The sum is then

$x+y=b+(x-z)=\underline{1}\,\underline{x-z}.$

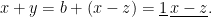
So this is a Léo-pair if and only if

$xy=\underline{x-z}\,\underline{1}.$

This equation, in terms of $x$ and $z$ , becomes

$x(b-z)=b(x-z)+1,$

which holds if and only if 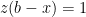$z(b-x)=1$ . Since the factors are integers and non-negative, this is only possible if 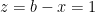$z=b-x=1$ , which means $x=y=b-1$ , the solution found by Léo.

Now suppose there is no carry. This means that we have 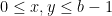$0\leq x,y\leq b-1$ and $x+y\leq b-1$ . Then
$x+y=\underline{0}\,\underline{x+y},$
and we have a Léo-pair if and only if
$xy=\underline{x+y}\,\underline{0},$
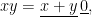
i.e., if and only if 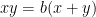$xy=b(x+y)$ .

This is not an uninteresting little equation! For a fixed 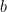$b$ (which could now be any non-zero rational), this defines a simple quadratic curve. Without the restrictions on the size of the solution 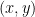$(x,y)$ , there is always a point on this curve, namely
$(x_0,y_0)=(2b,2b).$
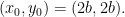
This does not fit our conditions, of course. But we can use it to find all other integral solutions, as usual for quadratic curves. First, any line through 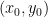$(x_0,y_0)$ intersects the curve in a a second point, which has rational coordinates if the line is also defined by rational coefficients, and conversely.

Doing this, some re-arranging and checking leads to the parameterization

$\begin{cases} x=b+k\\ y=b+\frac{b^2}{k}\end{cases}$

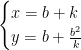
of the rational solutions to 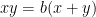$xy=b(x+y)$ , where 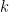$k$ is an arbitrary non-zero rational number. In this case, this can also be found more easily by simply writing the equation in the form
$0=xy-bx-by=(x-b)(y-b)-b^2\ldots$

Now assume that 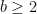$b\geq 2$ is an integer, and we want 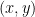$(x,y)$ to be integers. This holds if and only if 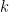$k$ is an integer such that $k\mid b^2$ .

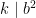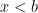Such solutions certainly exist, but do they satisfy the digit condition? The answer is yes if and only if $k=-b$ , which means $x=y=0$ , giving the expected degenerate pair. Indeed, to have $x<b$ , the parameter 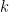$k$ must be a negative divisor of 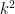$k^2$ . We write $k=-d$ with $d\mid k^2$ positive. Then to have non-negative digits, we must have
$\begin{cases} x=b-d\geq 0\\ y=b-\frac{b^2}{d}\geq 0\end{cases},$
the first one of these inequalities means $b\geq d$ , while the second means that $b\leq d$ …

The discrete spectrum is discrete

No, this post is not an exercise in tautological reasoning: the point is that the word “discrete” is relatively overloaded. In the theory of automorphic forms, “discrete spectrum” (or “spectre discret”) is the same as “cuspidal spectrum”, and refers to those automorphic representations (of a given group $G$ over a given global field $F$ ) which are realized as closed subspaces of the relevant representation space on $L^2(G(\mathbf{Q})\backslash G(\mathbf{A}_F))$ , by opposition with the “continuous spectrum”, whose components may fail to be actual subrepresentations.

However, we can also think of automorphic representations as points in the unitary dual of the relevant adélic group $G(\mathbf{A}_F)$ , and this has a natural topology (the Fell topology), for which it then makes sense to ask whether the set of all cuspidal automorphic representations is discrete or not.

The two notions might well be unrelated: for instance, if we take the group $\mathrm{SL}_2(\mathbf{R})$ and the direct sum over $t\in\mathbf{Q}$ of the principal series with parameter $t$ , we obtain a representation containing only “discrete” spectrum, but parameterized by a “non-discrete” subset of the unitary dual.

It is nevertheless true that the discrete spectrum is discrete in the unitary dual, in the automorphic case. I am sure this is well-known. (Unless the topology on the unitary dual is much weirder than I expect; my expertise in this respect is quite limited, but I remember asking A. Venkatesh who told me that the pathologies of the unitary dual topology are basically irrelevant as far as the automorphic case is concerned). I think this must be well-known, but I don’t remember seeing it mentioned anywhere (hence this post…)

Here is the argument, at least over number fields, and for $\mathrm{GL}_n$ . Let $\pi$ be a given cuspidal representation. The unitary dual topology on the adélic group is, if I understand right, the restricted direct product topology with respect to the unramified spectrum. So a neighborhood of $\pi$ is determined by a finite set $S$ of places and corresponding neighborhoods $U_s$ of $\pi_s$ for $s\in S$ . We want to find such a neighborhood in which $\pi$ is the unique automorphic cuspidal representation.

First, we can fix a neighborhood $U_{\infty}$ of the archimedean (Langlands) parameters that is relatively compact. Next, we note (or claim…) that for a finite place $v$ , the exponent of the conductor is locally constant, so we get neighborhoods $U_v$ of $\pi_v$ , with $U_v$ the unramified spectrum when $\pi$ is unramified at $v$ , such that all automorphic representations in
$U=U_{\infty}\times \prod_{v} U_v$
have arithmetic conductor equal to that of $\pi$ . With the archimedean condition, it follows that the Iwaniec-Sarnak analytic conductor of cuspidal representations in $U$ is bounded.

However, a basic “height-like” property is that there are only finitely many cuspidal representations with bounded analytic conductor (this is proved by Michel-Venkatesh in Section 2.6.5 of this paper, and a different proof based on spherical codes, as suggested by Venkatesh, is due to Brumley). Thus $U$ almost isolates $\pi$ , in the sense that only finitely many other cuspidal representations can lie in $U$ . Denote by $X$ this set of representations.

Now, the unitary dual is (or should be…) at least minimally separated so that, for any two cuspidal representations $\pi_1$ and $\pi_2$ , there is an open set which contains $\pi_1$ and not $\pi_2$ , say $V_{\pi_1,\pi_2}$ . Then
$U'=U\cap \bigcap_{\rho\in X-\{\pi\}} V_{\pi,\rho}$
is an open neighborhood of $\pi$ which only contains the cuspidal representation $\pi$ …

More conjugation shenanigans

After I wrote my last post on the condition $\xi H\xi =H$ in a group, I had a sudden doubt concerning the case in which this arose: there we assume that we have a coset $T=\xi H$ such that $g^2\in H$ for all $g\in T$ . I claimed that this implies $\xi H \xi =H$ , but really the argument I wrote just means that $\xi H \xi \subset H$ : for all $g\in H$ , we get $\xi g \xi g \in H$ , hence $\xi g \xi \in H$ . But what about the other inclusion?

I had in mind a case where the groups involved are finite, or close enough, so that the reverse inclusion is indeed obviously true. But it is amusing to see that in fact what I wrote is correct in all cases: if $H$ is a subgroup of an arbitrary group $G$ and $\xi\in H$ satisfies $\xi H \xi\subset H$ , then in fact $\xi H \xi = H$ : taking the inverse of the inclusion gives $\xi^{-1} H\xi^{-1}=\xi^{-1}H^{-1}\xi^{-1}\subset H^{-1}=H.$

I find this interesting because, when it comes to the normalizer, the analogue of this fact is not true: the condition $\xi H\xi^{-1}\subset H$ is not, in general, equivalent with $\xi H\xi^{-1}=H$ .

(I found this explained in an exercise in Bourbaki, Algèbre, Chapitre I, p. 134, Exercice 27, or page 146 of the English edition; here is a simple case of the counterexample from that exercise: consider the group $G$ of permutations of $\mathbf{Z}$ ; consider the subgroup $H$ which is the pointwise stabilizer of $\mathbf{N}=\{0,1,2,\ldots\}$ , and the element $\xi\in G$ which is just
$\xi(x)=x+1.$

Then we have $\xi H\xi^{-1}\subset H$ , because the left-hand side is the pointwise stabilizer of $\xi(\mathbf{N})$ which is a subset of $\mathbf{N}$ . But $\xi H\xi^{-1}$ is not equal to $H$ , because $\xi^{-1} H\xi$ is the pointwise stabilizer of $\xi^{-1}(\mathbf{N})$ , and there are elements in $G$ which fix $\mathbf{N}$ but not $\xi^{-1}(\mathbf{N})=\{-1,0,1,\ldots\}$ .)

It seems natural to ask: what exactly is the set $X$ of all $(a,b)\in\mathbf{Z}^2$ such that $\xi^a H\xi^b\subset H$ is equivalent to $\xi^a H \xi^b=H$ ? This set $X$ contains the line $(n,n)$ for $n\in\mathbf{Z}$ , and also the coordinates axes $(n,0)$ and $(0,n)$ (since we then deal with cosets of $H$ ).

In fact, one can determine $X$ : it is the complement of the line $(n,-n)$ , for $n\not=0$ (which corresponds to conjugation). Indeed, suppose for instance that $a+b\geq 1$ . Let $H$ and $\xi$ be such that $\xi^a H \xi^b\subset H$ .

We can write
$-a=(a+b-1)a-a(a+b),\quad\quad -b=(a+b-1)b-b(a+b),$
and
$\xi^{-a}H\xi^{-b}=\xi^{(a+b-1)a} (\xi^{a+b})^{-a}H (\xi^{a+b})^{-b} \xi^{(a+b-1)b}.$
Since $\xi^{a+b}\in H$ , and since $a+b-1\geq 0$ is the common exponent of $\xi^a$ and $\xi^b$ at the two extremities of the right-hand side, it follows that this right-hand side is contained in $H$ .

A similar argument works for $a+b\leq -1$ , using
$-a=(-a-b-1)a+a(a+b),\quad\quad -b=(-a-b-1)b+b(a+b),$
where again it is crucial that the coefficient $(-a-b-1)$ appears on both sides, and that it is $\geq 0$ .

Since we already know that $(1,-1)\notin X$ , and in fact that $(-n,n)\notin X$ for $n\not=0$ (the same setting as the counterexample above works, because the $\xi$ we used is an $n$ -th power for every $n\not=0$ ), we have therefore determined the set $X$ …

Normalizers everywhere

In working on a paper, I found myself in the amusing but unusual situation of having a group $G$ , a subgroup $H$ and an element $\xi\in G$ such that
$\xi H\xi =H.$

This certainly can happen: the two obvious cases are when $H=G$ , or when $\xi$ is an involution that happens to be in the normalizer $N(H)$ of $H$ .

In fact the general case is just a tweak of this last case: we have $\xi H\xi=H$ if and only if $\xi^2\in H$ and $\xi\in N(H)$ , or in other words, if $\xi$ belongs to the normalizer, and is an involution modulo $H$ .

This is of course easy to check. I then asked myself: what about the possibility that
$\xi^a H\xi^b = H$ ,
where $a$ and $b$ are arbitrary integers? Can one classify when this happens? The answer is another simple exercise (that I will probably use when I teach Algeba I next semester): this is the case if and only if $\xi^{a+b}\in H$ and $\xi^{(a,b)}\in N(H)$ , where $(a,b)$ is the gcd of $a$ and $b$ . In particular, for all pairs $(a,b)$ where $a$ and $b$ are coprime, the condition above implies that $\xi$ belongs to the normalizer of $H$ .

Here is the brief argument: having fixed $\xi$ , let
$M=\{(\alpha,\beta)\in\mathbf{Z}^2\,\mid\, \xi^{\alpha}H\xi^{\beta} =H\}.$
This set is easily seen to be a subgroup of $\mathbf{Z}^2$ . Furthermore, note that $(\alpha,\beta)\in M$ implies that $\xi^{\alpha+\beta}\in H$ , which in turns means that $(\alpha+\beta,0)\in M$ and $(0,\alpha+\beta)\in M$ .

Hence if $(a,b)\in M$ , we get
$(a,-a)=(a,b)-(0,a+b)\in M,\quad\quad (b,-b)=(a+b,0)-(a,b)\in M$ ,
so that
$M\cap (1,-1)\mathbf{Z}$
contains $(a,-a)\mathbf{Z}\cap (b,-b)\mathbf{Z}$ , which is just
$(d,-d)\mathbf{Z},$
where $d=(a,b)$ . But $(d,-d)\in M$ means exactly that $\xi^{d}\in N(H)$ .

Thus we have got the first implication. Conversely, the conclusion means exactly that
$(a+b,0)\in M,\quad (d,-d)\in M.$
But then
$(a,b)=(a+b,0)-(b,-b)=(a+b,0)-b/d (d,-d)\in M$
shows that $\xi^a H\xi^b=H$ .

To finish, how did I get to this situation? This can arise quite naturally as follows: one has a collection $X$ of representations $\rho$ of a fixed group $\Gamma$ , and an action of a group latex $G$ on these representations $X$ (action up to isomorphism really).
For a given representation $\rho_0$ , we can then define a group
$H=\{g\in G\,\mid\, g\cdot \rho_0\simeq \rho_0\}$
and also a subset
$T=\{g\in G\,\mid\, g\cdot \rho_0\simeq D(\rho_0)\},$
where $D(\cdot)$ denotes the contragredient representation.

It can be that $T$ is empty, but let us assume it is not. Then $T$ has two properties: (1) it is a coset of $H$ (because $H$ acts on $T$ simply transitively); (2) we have $g^2\in H$ for all $g\in T$ (because the contragredient of the contragredient is the representation itself).

This means that, for some $\xi\in G$ , we have $T=\xi H$ , and furthermore
$\xi H\xi=H$
since $\xi g\xi g\in H$ for all $g\in H$ .

By the previous discussion, we therefore get a good handle on the structure of $T$ : either it is empty, or it is of the form $\xi H$ for some $\xi\in G$ such that $\xi^2\in H$ and $\xi$ normalizes $H$ in $G$ . In particular, if $H$ is trivial (which happens often), either $T$ is empty, or it consists of a single element $\xi$ which is an involution of $G$ .