Mathematics – Page 47 – E. Kowalski's blog

The Kochen-Specker argument, and the spectral theory script

Somewhat later than I had hoped, I have updated the script of my spectral theory course. The version currently found online is complete as far as the material I intended to put in is concerned, but there are a few places where I haven’t written down all details (in particular for the proof of the Weyl law for the Dirichlet Laplace operator in an open subset of Euclidean space). I am also aware of quite a few small problems in the last chapter on Quantum Mechanics, due partly to notation problems (for the Fourier transforms, and for “physical” versus mathematical normalizations). I will need to re-read the whole text carefully to correct this; on the other hand, thanks to lists of corrections that I have already received from a few students, the number of typos is much less than before… I will however continue updating the PDF file as I continue checking parts of the text.

What delayed this version for a long time was the write-up of the last section on “The interpretation of Quantum Mechanics”; of course it’s in some sense an extraneous part of the script, since spectral theory barely enters in it, but I found it important to at least try to connect the mathematical framework with the actual physics. (This partly explains all the reading I’ve done recently about these issues). It is equally obvious that I am not the most knowledgeable person for such a discussion, but after all, there are good authorities that claim that no one really understands this question anyway…

What I end up discussing contains however one little mathematical result, which is cute and interesting independently of its use in Quantum Mechanics; it is a theorem of S. Kochen and E.P. Specker which states the following:

There does not exist any map
$f\,:\, \mathbf{S}^2\rightarrow \{0,1\}$
where S² is the sphere in R³ with the property that, whenever
$x,y,z$
are pairwise orthogonal unit vectors, we have
$f(x)+f(y)+f(z)=2$
or in other words, two of the three values are equal to 1, and the other is equal to 0.

How this result enters into discussions of the interpretation of Quantum Mechanics is described by M. Jammer in his book on the subject (not the same as his book on the development of Quantum Mechanis, but another one, equally evanescent as far as the internet is concerned); more recently, J. Conway and S. Kochen have combined it with the Einstein-Podolsky-Rosen argument (or paradox) to derive what they call the “Free Will Theorem”, which is an even stronger version of the unpredictability of properties of Spin 1 particles (those to which the Kochen-Specker argument applies). Conway has given lectures in Princeton on this result and its history and consequences, which are available as videos online.

Coming back to the result above, considered purely from the mathematical point of view, it is interesting to notice that both the original proof and the version used by Conway-Kochen (which is due to A. Peres) show that the hypothetical map does not exist even for some finite sets of points on the sphere. It is of some interest to get a smallest possible set of such points. The proof I gave in the script, however, which is taken from Jammer’s book (who attributes it to R. Friedberg) is maybe theoretically slightly more complicated, but it is also somewhat more conceptual in that one doesn’t have to be puzzled so much at the reason why one finite set of vectors or another is really fundamental.

Kronecker-Weber by deformation, or: another bad reference

I have already mentioned two instances of pretty bad references in which I am involved (here and there). Here’s a third one: in Remark I.5.4 in my introductory notes on automorphic forms, L-functions and number theory (published in the proceedings of a school held at the Hebrew University in Jerusalem in March 2001), I state

Remark 1.5.4. The Kronecker-Weber Theorem, as stated here, bears a striking resemblance
to the L-function form of the modularity conjecture for elliptic curves (explained
in de Shalit’s lectures). One can prove Theorem 1.5.2 by following the general principles of
Wiles’s argument [Tu] (deformation of Galois representations, and computation of numerical
invariants in a commutative algebra criterion for isomorphism between two rings).

where the helpful-looking [Tu] leads rather disappointingly to:

[Tu] Tunnell, J.: Rutgers University graduate course (1995–96).

About a year and a half ago, R. Rhoades asked me if there was any more information available about this. The answer was that I had my own handwritten lecture notes of the original course taught by J. Tunnell at Rutgers (of course, maybe other people who had participated had their own). I said that I’d try to get those notes scanned, but it’s only in the last two days that I’ve finally started doing so — thanks to the recent installation in the ETH Library of a pretty fancy scanning machine, which makes the process essentially painless.

I’ve only scanned the first notebook and part of the second for the moment (enough to contain what Tunnell did about the GL(1) analogue of the modularity theorem of Wiles and its application to the Kronecker-Weber theorem):

First notebook

Second notebook

Unfortunately, it’s not clear how useful these will be to anyone, except future historians of the teaching of the proof of Fermat’s Great Theorem. The lectures are not entirely linear (there are notes about a parallel seminar on Serre’s Conjecture and of a few other lectures in the middle), they are in French, and the quality of the scan is not perfect (the second notebook was particularly cheap, and the ink on one side of a page is partly visible on the other side).

Qui dit mieux?

Analytic number theorists often work with multiple sums and integrals. In fact, sums are sometimes so congenial that the more there are, the merrier, and it may be quite a deep step to split a single sum into two. A famous examples is found, for instance, in Iwaniec’s celebrated bilinear form of the remainder term in the linear sieve, where one goes from something like

$\sum_{d<D}{|r_d|}$

to an expression involving two variables (say n and m)

$\sum_{m<M}{\sum_{n<N}{\alpha_m\beta_n r_{mn}}}$

with

$MN=D,$

and more or less unknown (but essentially bounded) coefficients α and β. (For a very clear discussion of why this is of crucial importance in some important problems of analytic number theory, and why the second form is more useful than the first, see for instance the Section entitled “The remainder term” in this survey paper of J. Friedlander).

In this spirit of increasing sums unboundedly, here is the record-holder I’ve seen so far (if memory serves): it is equation (29) in a paper of M. Young on non-vanishing of central values of L-functions of elliptic curves. Here is a screenshot:

where one counts no less than 11 summation signs.

Does any reader have a better example at hand? Examples involving the composition of more than 11 derived functors are also welcome for this friendly competition.

Felicities of the German language

In supermarkets in Zürich (and in other German-speaking parts of the world), aluminium foil is called “Aluminiumfolie” — fairly straightforward, certainly, but since the word “folie” means “madness” in French, every time I see this word, I can’t help thinking of a some kind of craze for aluminium that would justify a name like “aluminium madness”.

Similarly, the word “Art” in German does not mean what the spelling suggests (which is “die Kunst”); much more mundanely, it means “kind” as in “integral of the third kind” or “Stirling-Zahlen zweiter Art”. But, even more than for aluminium, whenever I read a title like

Über eine neue Art von nichtanalytischen automorphen Funktionen und die Bestimmung Dirichletscher Reihen durch Funktionalgleichungen

I can not help translating it as

A new art of non-holomorphic automorphic functions and the determination of Dirichlet series by functional equations

(this is the paper where Hans Maass first introduced what are now called Maass forms, and showed how these non-holomorphic modular forms could lead to Dirichlet series with functional equation related to real quadratic fields, in analogy with the case of imaginary quadratic fields where holomorphic forms occured — both are now understood as cases of “Langlands functoriality”).

Equally romantic is Emil Artin’s title

Über eine neue Art von L-Reihen

for the paper where he introduces what are now called Artin L-functions; translating it as “On a new art of L-functions” seems so much better than just “On a new kind of L-functions”…

Torsion in the homology of 3-manifolds

[The post has been slightly edited to clarify some issues of identification of people, as mentioned in the first comment (24-6-09)].

The topic of this post is obviously rather far from my usual fields of expertise, but since I’ve actually used the large sieve to say something about this topic, and since I was reminded of it by the excellent talk of A. Venkatesh during the Bruggeman conference, here are a few words…

The first thing to say is that whereas the topic may seem a tad abstract and a bit far from good old analytic number theory, this is not really true. In fact, in the cases described by Venkatesh (which corresponds to — separate — joint work with F. Calegari and N. Bergeron, and concern hyperbolic arithmetic 3-manifolds), what is involved can be made extremely concrete. Indeed, to get examples, one can take an imaginary quadratic field K, an integral ideal n in K, and ask about the structure of the finitely-generated abelian group defined as the abelianization

$\Gamma_0(\mathbf{n})^{ab}=\Gamma_0(\mathbf{n})/[\Gamma_0(\mathbf{n}),\Gamma_0(\mathbf{n})]\subset$

of the congruence subgroup

$\Gamma_0(\mathbf{n})=\{\left(\begin{array}a&b\\c&d\end{array}\right)\quad,\quad \mathbf{n}\mid c\}\subset PGL(2,\mathbf{Z}_{K})$

(using the “Bordeaux” notation for the ring of integers of K; amusingly, it seems the post I once wrote on this subject has disappeared, although I could still find a link to it on Google).

The link with homology is that this abelianization is well-known (by the Hurewicz theorem) to be isomorphic to the first homology group

$H_1(X_{n},\mathbf{Z})=H_1(\Gamma_0(\mathbf{n}),\mathbf{Z})$

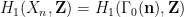
of the quotient manifold of the hyperbolic three space H₃ by the discrete group:

$X_{\mathbf{n}}=\Gamma_0(\mathbf{n})\backslash \mathbf{H}_3$

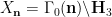
(speaking of notation, I noticed that Venkatesh behaved like an un-reconstructed right-winger in putting his discrete group on the right-hand side).

One outcome of the ongoing work that Venkatesh discussed (still partly conjectural, and encompassing much larger classes of examples) is the fact that the size of the torsion part of these groups tends to be “as large as possible”. As Venkatesh explained, this means roughly that this torsion group is of order exponential with respect to the norm of the ideal n, which is interpreted as being roughly (up to multiplicative constants) the volume of the manifold. The fact that this is the fastest possible type of growth follows from the interpretation of the size of the homology groups (when finite, at least) as the determinant of integral matrices which have only a bounded number of bounded non-zero entries in each row and column (as n varies). A convincing numerical example was given: the torsion subgroup for an ideal of norm about 500 (if I remember right) for

$K=\mathbf{Q}(\sqrt{-2}),$

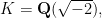
was roughly of order

$10^{80}.$

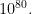
What I had done on this torsion topic, as explained in Section 7.6 of my almost famous book on the large sieve (and also, though with some uncorrected typos, in a preliminary short note), was to show how, in the model of random (compact connected orientable) 3-manifolds suggested by N. Dunfield and W. Thurston, something quite similar was happening with high probability.

More precisely, the 3-manifolds of Dunfield and Thurston are obtained as follows: one fixes first an integer g at least 2, then a symmetric set of generators of the mapping class group Γ_g of a closed (topological) surface of genus g, then one forms the random walk on this discrete group (where the generators are chosen uniformly and independently), getting a sequence

$\varphi_0=1,\quad \varphi_k=\xi_1\cdots \xi_k,$

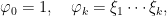
of random variables, each of which lives in the mapping class group. Because the latter is a big complicated non-abelian group (as can be seen, for instance, quite naively from the important fact that it has a natural surjection

$\Gamma_g\rightarrow Sp(2g,\mathbf{Z}),$

to an integral symplectic group), this random walk is highly transient and “escapes to infinity” quickly. Now, to get from these surface maps to 3-manifolds, one uses “Heegard splittings”: given any mapping class φ, take two filled “handlebodies” of genus g (which are compact 3-manifolds with boundary, the boundary being a standard surface of genus g), then glue them together by identifying the two boundaries (which are, topologically, the same surface) with the help of the homeomorphism φ. [This procedure was invented as early as 1898 by Heegaard; personally, I have the greatest trouble visualizing it, and this has the effect that I find extremely puzzling the proofs I have seen of the fact that any compact 3-manifold can be obtained in this way, at least for some g, since it is more or less treated as close to trivial once the 3-manifold is triangulated…]

In any case, for a 3-manifold presented as a Heegaard splitting of genus g, the abelianization of the fundamental group of the resulting manifold M_φ turns out to be easy to describe in terms of the mapping class used for the identification of the handlebodies: we have

$H_1(M_{\varphi},\mathbf{Z})\simeq \mathbf{Z}^{2g}/\langle J,\varphi^*J\rangle,$

for some lattice J in Z^2g, where the mapping class acts from the fact that the homology of the boundary surface of genus g is a free group of rank 2g.

This formula suggests that, “generically”, the homology group of a 3-manifold should be finite, because, equally generically, the lattice J and its image under the mapping class should be transverse and generate the whole Z^2g together. This was checked qualitatively by Dunfield and Thurston, and using sieve, it was not hard to provide an exponential decay of the probability that the homology is infinite. Then, the main point, already explained by Dunfield and Thurston, is that after fixing a prime p, the analogue formula

$H_1(M_{\varphi},\mathbf{F}_p)\simeq \mathbf{F}_p^{2g}/\langle J\otimes\mathbf{F}_p,\varphi^*(J\otimes\mathbf{F}_p)\rangle$

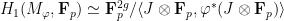
holds for the homology with coefficient in the finite field with p elements, which is also equal to

$H_1(M_{\varphi},\mathbf{F}_p)=H_1(M_{\varphi},\mathbf{Z})\otimes \mathbf{F}_p.$

However, there is now a definite probability, of size roughly 1/p, that this homology group be non-zero (roughly, it is the probability that a determinant modulo p, which is mostly equidistributed, vanish). Because the series of 1/p over primes diverges, it follows that, intuitively, the first homology group of a random 3-manifold (in their sense at least) is typically finite, but is divisible by many primes (and hence is quite large).

Making this quantitative (as I did) is not particularly difficult once the large sieve is properly setup in discrete groups with Property (T) (or, in that case, for those having a quotient with property (T), namely the symplectic group Sp(2g,Z); Andersen has shown that the mapping class group itself does not have this property), and it leads to the conclusion that, with probability exponentially close to 1 as the length of the random walk increases, the first homology group is finite with order divisible by roughly

$\log k$

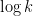
distinct primes. This implies (by Chebychev-type estimates) a growth which is superpolynomial but potentially less than exponential, namely the size should be at least

$k^{\alpha\log\log k}$

for some constant α>0, with probability close to 1. If one could show that the primes dividing the order are not always too small (a property which, by the way, was clearly visible in the example shown by Venkatesh, with some fairly large primes appearing), it would follow that the size should be exponential in k, since this is the typical size of an integer with that many prime factors.

At this point one may object that this parameter k, the length of the random walk, is not a good parameter to measure the 3-manifold M_{φ_k} with, because it not canonical at all. In fact, although all (compact connected orientable) 3-manifolds have a Heegaard splitting, its genus g can not be chosen at will (one can not always take g=2, as far as I understand, though apparently this is possible for many 3-manifolds, this being related with the minimal number of generators of the fundamental group). Moreover, for a given genus, there are many choices of generating sets to define the random walk, and even then the random walk might come back a few times to the same 3-manifold with different values of k, etc… This suggested that only the asymptotic behavior (as the length of the walk grows) of things like the average number of coverings of the manifold with a given Galois group, etc, really carried significance (such numbers were computed precisely in the paper of N. Dunfield and W. Thurston).

The talk of Venkatesh reminded me of one possible rough interpretation of k, which I vaguely remembered from the paper of Dunfield and Thurston: it is the content of what they state as Conjecture 2.11 (page 12), which says that, with high probability, the random 3-manifold should be hyperbolic, and that its expected volume should grow linearly with k. And if we interpret k as a succédané of the volume, then an exponential lower bound corresponds exactly to the growth conjectured by Bergeron and Venkatesh, while the almost exponential one obtained from the sieve gives strong evidence for it being, indeed, “generic”. [Their manifolds being of a special type, the generic case does not apply directly, of course.]

Here I would have been happy to give some convincing comments on the status of this conjecture of Dunfield and Thurston. J. Maher has a preprint where he proves the hyperbolicity statement, but the proof depends on the geometrization conjecture of Thurston which was, of course, proved by (the methods of) Perelman. Maher also states that the volume part follows then from his result and a work of Brock and Souto, but a web search only reveals this paper to be “in preparation”; added to the fact that I can not claim to understand even Maher’s proof, I feel more comfortable simply saying that it seems that the statement may well be on the verge of being proved. [Any more informed comments will be extremely welcome!]

I would like to conclude by saying that although this is not my area, I found it to be fairly accessible, at an intuitive level, by virtue of the existence of very good surveys and expositions online, e.g., this book-in-progress of Farb and Margalit, and the paper of Dunfield-Thurston, which is very readable.