In the next few posts, I want to describe some aspects of the paper “Algebraic twists of modular forms and Hecke orbits” that I just finished with Étienne Fouvry and Philippe Michel. Today, I will describe some cases of the main result (I was thinking of continuing dans la foulée with a high-level sketch of the proof, but it seems better to delay this until the next time…)
I’ll start with one of the simplest cases, which was also one of our original challenges. Let  be a classical holomorphic modular form, say of level
be a classical holomorphic modular form, say of level 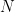 and weight
and weight 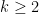 , with Fourier expansion
, with Fourier expansion

for  in the upper half-plane. If in doubt, you may assume that
in the upper half-plane. If in doubt, you may assume that
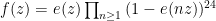
is the Ramanujan 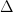 -function, with
-function, with 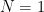 and
and 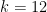 .
.
The (normalized) Fourier coefficients 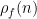 are essentially bounded (they are bounded in mean-square norm over
are essentially bounded (they are bounded in mean-square norm over 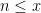 , by Rankin-Selberg theory) and their signs oscillate quite randomly. In particular, one expects that sums of the type
, by Rankin-Selberg theory) and their signs oscillate quite randomly. In particular, one expects that sums of the type

should be rather small, unless 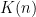 is itself somehow related to
is itself somehow related to 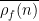 .
.
Our question was: can we prove that this is the case when we take  , a prime number, and
, a prime number, and
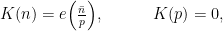
(where we denote by 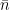 the multiplicative inverse modulo
the multiplicative inverse modulo  of some integer
of some integer 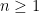 coprime with
coprime with  )?
)?
One can indeed ask this as a challenge: considering that we feel that we know something about Fourier coefficients of modular forms, shouldn’t we be able to prove that they do not correlate with  ? (In addition, there is a geometric motivation, which I will defer to another post.)
? (In addition, there is a geometric motivation, which I will defer to another post.)
It is a very simple and special case of our results that, indeed, we can do something with such sums. Precisely, we prove that
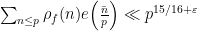
for any prime  and for any
and for any 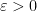 , where the implied constant depends on
, where the implied constant depends on  and
and  .
.
The more general statements are all of the following type: for a prime  , we have some “weight”
, we have some “weight” 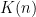 defined for
defined for  modulo
modulo  , which we extend to all of
, which we extend to all of 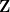 by composing with reduction modulo
by composing with reduction modulo  . Then we want to bound from above the sum
. Then we want to bound from above the sum

for a fixed  . Our results are of the form
. Our results are of the form

where the implied constant depends only, as before, on  and
and 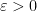 , and where the dependency on
, and where the dependency on 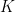 is contained entirely in the quantity
is contained entirely in the quantity  , which I will only define precisely in later instalments, but which roughly speaking measures how difficult it is to express
, which I will only define precisely in later instalments, but which roughly speaking measures how difficult it is to express 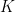 as a linear combination of special coefficients which I will call here simply “of algebraic origin”.
as a linear combination of special coefficients which I will call here simply “of algebraic origin”.
In fact, we do not express the result in this manner. A technical difference is that we use smoothed sums, proving bounds like

where 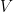 is a smooth function compactly supported on
is a smooth function compactly supported on ![[0,1] [0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=000000&s=0) and the implied constant now also depends on
and the implied constant now also depends on 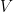 , but in very controlled ways. Moreover, we concentrate on the special coefficients of algebraic origin, leaving the general case to the triangle inequality. For instance, our previous weight
, but in very controlled ways. Moreover, we concentrate on the special coefficients of algebraic origin, leaving the general case to the triangle inequality. For instance, our previous weight
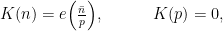
is of algebraic origin for every prime  , with
, with  absolutely bounded, and hence the first result is a consequence of the more general case. Another more general type of examples (which remains far from the most general!) is given by
absolutely bounded, and hence the first result is a consequence of the more general case. Another more general type of examples (which remains far from the most general!) is given by

for integral polynomials  ,
, 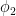 , and for a Dirichlet character
, and for a Dirichlet character  modulo
modulo  . All of these are “of algebraic origin”, and when
. All of these are “of algebraic origin”, and when 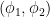 are fixed, the norm
are fixed, the norm  is uniformly bounded as
is uniformly bounded as  varies. Note in particular that
varies. Note in particular that  is possible, and it is certainly among the most natural examples. Indeed, the smoothed form of our bounds leads by classical means to a subconvex estimate for twisted L-functions, which is of the type
is possible, and it is certainly among the most natural examples. Indeed, the smoothed form of our bounds leads by classical means to a subconvex estimate for twisted L-functions, which is of the type
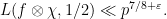
This is not new, but it illustrates the range and depth of our results. (Such a bound, with a weaker exponent, was first proved by Duke-Friedlander-Iwaniec, and the exponent 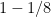 was first obtained by Blomer and Harcos, refining a method of Bykovski.)
was first obtained by Blomer and Harcos, refining a method of Bykovski.)
Before finishing for today, here is one example that suggests how one may go well beyond those previously considered. For  prime and
prime and  ,
, 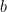 coprime with
coprime with  , let
, let

be the classical Kloosterman sum. Then the weights

are “of algebraic origin”. Applying our methods to the second one, we end up with the question discussed in the previous post…