Here’s another funny question about the English language: what is the sequence of three letters XYZ (where X, Y and Z are among the 26 letters of the alphabet) such that the number of correct (English) words of the form TXYZ is maximal, where T is just another letter? In this, it seems also best to assume that the last letter Z is not “s”, since the latter allows for many plurals of what are really three-letter words.
I think that, depending on the dictionary used (in particular, archaic words can be quite common among short words like this, and will only appear in the OED), the answer is between 13 and 17. The dictionary on my laptop (aspell-0.60-en) gives one word with 13 (say TWR), two with 12 (say BGA and IPX), and a few ending with “s”. The ending TWR jumps to 17 when permitted to appeal to the OED, and so does BGA. However, IPX only goes to 13.
Answers next week if nobody tries his/her hand first at the solution…
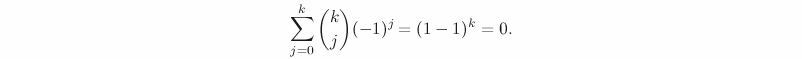
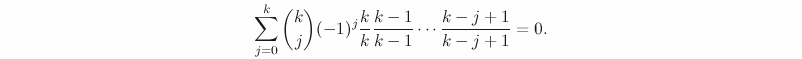
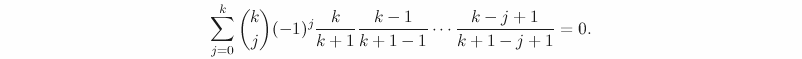
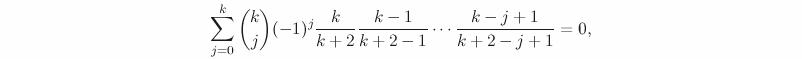
![[LaTeX text]](http://blogs.ethz.ch/kowalski/files/2008/02/a.png)