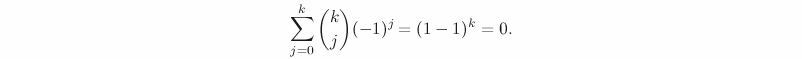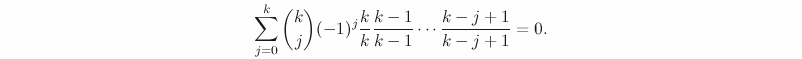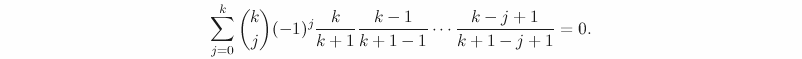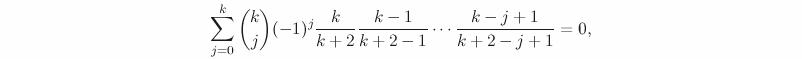I did a post a while ago on some “bad” mathematical terminology. I will here modestly continue with an example from my own work. Already a few years ago, I wrote a paper on some local-global questions where, among other things, I introduced something called a “fairly well-spread point” on a commuative algberaic group (defined over a number field). Some recent work of A. Perucca shows that this condition, for a point P in a simple abelian variety A/K is equivalent with asking that the Zariski closure of the subgroup generated by P is equal to A, a condition so natural that it deserves a better name (though she mentioned that some other people call this “independent”, which is also quite bad in its way).
To defend myself, the context of the definition for me was that I was trying to prove a certain theorem as cleanly as possible for as many algebraic groups as possible, and I had found that an even stronger condition (being “well-spread”) gave a nice proof, without undue tricks. But that condition is almost certainly true only in the case of (infinite order) points on elliptic curves or the multiplicative group (though I’m not sure if counter-examples are actually known), and I observed that only three consequences of the well-spread condition were used, leading to “fairly well-spread”. Since the three conditions were pretty ugly looking, I didn’t want to emphasize them. But the results of Perucca show I didn’t dig far enough to understand the true mechanisms involved…
But now I would like to point out something which, I think, my paper did right, compared with a number of other related works around the same time (2000-2003), which were interested in the so-called support problem.
The original version of this problem, apparently due to Erdös, concerns two non-zero integers x and y, and asks whether
for all prime numbers p not dividing x or y, the (multiplicative) order of x modulo p is equal the order of y modulo p,
implies that x=y.
This was first solved explicitly around 1995 by Corrales Rodrigáñez and Schoof, with an affirmative answer, and in a more general case (as described below).
What I think was useful in my contribution in this problem was to find a more intrinsic-looking variant, that makes sense in greater generality, and (probably) has a “cleaner” answer.
The first natural generalization that comes to the mind (I guess) of most algebraically inclined arithmeticians would be: for a commutative algebraic group G/K defined over a number field, and two rational points P and Q of G(K), what does the condition
for almost all prime numbers p of the ring of integers of K, the order of Q modulo p divides the order of P modulo p,
imply for P and Q? Then the question before amounts to looking at the multiplicative group over Q and integral points on it. Note that the original condition is stronger in asking for information modulo all primes where it makes sense, whereas for a general group, it certainly is easier to try to avoid, if possible, having to introduce the “best” integral model to reduce at. It is also stronger in the assumption of equality of the orders, but one quickly comes to see that the one-sided divisibility assumption is more natural. It also means the answer has to be more complicated than P=Q, because it is clear that Q=f(P) works, for any endomorphism f of G (defined over K).
This question is the version in the work of Corrales Rodrigáñez and Schoof, who proved that indeed the example above is the only possibility (if the points are of infinite order) for the multiplicative group or for an elliptic curve.
My own version was the following: given an algebraic group G/K (arbitrary, though of finite type of course), and a single point P on G, let <<P>> be the set of all Q such that
for almost all prime numbers p of the ring of integers of K, Q modulo p is in the subgroup generated by P modulo p.
Then the question is to compute this set <<P>>, indeed this subgroup (it is clearly a subgroup).
This question is not the same question as before, a priori, except in the simple case of the multiplicative group: indeed, then Q is in <<P>> if and only if it satisfies the assumption of the support problem, because in a finite cyclic group (such as the group of invertible elements in a finite field), the subgroup generated by an element x is uniquely determined as the set of elements having order dividing that of x. So the result of Corrales Rodrigáñez and Schoof, and the fact that the only endomorphisms of the multiplicative group are “raising to some integral power”, imply that <<P>>=<P> for any such group. But the converse is also true! Because Schinzel had proved the desired conclusion for the second problem as far back as 1960 (at least over Q), it follows that the question of Erdös was solved 28 years before he raised it (there is a very cute proof by Gallagher, based on his highly ingenious larger sieve, about which I will probably post one day).
My own paper (among other not-too-closely related problems) proved that the same conclusion holds for elliptic curves, and some other abelian varieties (those with trivial endomorphism ring with dimension 2,6, or odd). The case of CM curves illustrates a different with the support problem, where the existence of CM endomorphisms really does affect the answer.
Now, why do I think that my version is a better question than the support problem or its variants? (A position which, it should be said, has not been adopted by the other people working around this type of problems, though there are some works which call this the “linear dependence problem”).
There are two reasons.
(1) I do not ask for a “Yes or No” answer, but I want to compute some subgroup, which clearly contains <P>; if it is bigger, then it’s an interesting phenomenon that should be noted and investigated (just as, even if the ring of integers in a number field is not principal, its ideal class group, which encodes “how far” it is from being principal, is of capital importance). For example, in the case of the additive group, <<P>> is the set of Q-multiples of P (so, it is strictly bigger than the set of integral multiples).
(2) The setting seems more intrinsic, somehow. To emphasize this, the following properties are easy to prove: <<P>> is a subgroup with some “functoriality” property, which doesn’t depend on the choice of either the group G or the field K, provided P is in G(K). (In particular, e.g., one can compute it for tori if the answer is known in the split case). In an Appendix to my paper, I found easy examples that illustrate that the set of points Q satisfying the assumptions of the support problem can fail any of these three properties (for instance, for the additive group, the set in question is all of K, for any non-zero P, so it depends on K).
The best general result concerning the problem of determining the “subgroup locally generated by P” is really due to T. Weston (working independently of me, and without the general terminology): he proved that the subgroup locally generated by n elements (defined by generalizing in the obvious way the case of n=1 above) in an abelian variety with trivial endomorphism ring is contained in the subgroup generated by those elements and by the torsion subgroup of A(K). Note that this conclusion is not quite satisfactory in view of the properties above: it is not invariant under field extensions (or replacing A but a bigger variety).
It is open, but conceivable that for any abelian variety A/K, and any rational point P on A, we have <<P>>=<P>. On the other hand, for the general support problem, Larsen showed first that Q must satisfy f(P)=cQ for some endomorphism f and non-zero constant c, and then found examples where c can not be taken to be 1. This depends non-trivially on the structure of A and of its subgroup of rational torsion points. So finding a “general formula” for the set of Q solving the support problem for a given P seems difficult.