Category: Mathematics

Minkowski’s classic theorem of “geometry of numbers” states that any convex subset of Rⁿ which is symmetric (with respect to the origin) and of volume (with respect to Lebesgue measure) larger than 2ⁿ contains a non-zero integral point.

This theorem is used, in particular, in the classical treatment of Dirichlet’s Unit Theorem in algebraic number theory. While teaching this topic last year, I wondered whether there was an hyperbolic analogue, in the following sense, where H is the hyperbolic plane in the Poincaré model:

does there exist a constant C such that any geodesically convex subset B of the hyperbolic plane H with hyperbolic area at least C which is geodesically symmetric with respect to the point i contains at least one point z of the form g.i, where g is an element of SL(2,Z) and g.i refers to the usual action by fractional linear transformations, with z not equal to i.

Here, the subset B is geodesically convex if it contains the geodesic segment between any two points, and symmetric if, whenever x is in B, the point on the geodesic from i to x which is at distance d(i,x) from i, but in the opposite direction, is also in B.

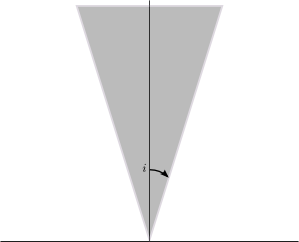
It turns out that the answer is “No”. Indeed, C. Bavard gave the following example:

let B be a euclidean half-cone with base vertex at 0, axis the vertical axis, and angle at the origin small enough, then B does not contain any “integral” point except i, but has infinite hyperbolic area. Moreover, it is easily seen that B is convex and symmetric in the hyperbolic sense, since hyperbolic geodesics are vertical half-lines and half-circles meeting the real line at right angles.

To check the claim, it is enough to show that for any integral point z=g.i distinct from  i, the ratio |x|/y has a positive lower bound, where z=x+iy (this will show that the angle from the vertical axis is bounded from below, so the point is not in a cone like the one above with sufficiently small angle). But z is given by (ai+b)/(ci+d) with a, b, c, d integers and ad-bc=1, and this ratio is simply |ac+bd|. Being an integer, either it is 0, or it is at least 1. Manipulating things, one checks that the first case only occurs for matrices in SL(2,Z) which are orthogonal matrices, and those fix i, so the point is then z=i. Hence, except for this case, the ratio is at least 1 and this concludes the argument.

It is interesting to see what breaks down in the (very simple) proofs of Minkowski’s theorem in the plane. In the first proof found on page 33 of the 5th edition of Hardy and Wright’s “An introduction to the theory of numbers” (visible here), the problem is that there is no way to dilate the convex region B in a homogeneous way compatible with the SL(2,Z) action. In other words, SL(2,Z) is essentially a maximal discrete subgroup of SL(2,R) (maybe it is maximal? I can’t find a reference).

Here is a striking example of the unfortunate (but probably unavoidable) dispersion of mathematics: at the end of the abstract of V. Arnold’s talk at the recent conference in honor of A. Douady, one can read:

The Cesaro mean values K̂ of the numbers K(n) tend, as n tends to ∞, to a finite limit K̂(∞)=lim 1/n ∑_m=1ⁿ K(m) = 15/π². This theorem, deduced from the empirical observation of the coincidence of 20 first digits, is now proved, using the formula K̂(∞)=ζ(2)/ζ(4)

Here, K(n) is defined before in the abstract as the expression

Arnold’s achievements as mathematician are about as impressive as it can get. But the statement here is a completely elementary exercise in analytic number theory, and has been for at least one century (i.e., Dirichlet, or Chebychev, could do it in a few minutes, if not Euler).  Here’s the proof in Chebychev style:

hence, exchaning the sum over n and the sum over d, we get

and replacing the integral part by X/d+O(1), this is clearly asymptotic to CX with

which is an absolutely convergent series. As an Euler product it is

as desired.

I have just read about the following very nice dichotomy: suppose we have an infinite set X, and a collection of subsets C in X; suppose further we look at all subsets F of X of finite size n, and at the subsets of F which can be defined by intersection of F with an element of C. How rich can this collection of subsets of F be, as F varies over all subsets of fixed (but growing) size?

For example, X could be the real line, and C the collection of half-lines ]-∞,a]. Then if we enumerate the finite subset F in increasing order

the subsets we obtain by intersecting with C are rather special: apart from the emptyset, we have only the n subsets of elements in increasing order up to some a:

with r≤n. In particular, there are only n+1 subsets of F which can be obtained in this manner, much less than the 2ⁿ subsets of F.

As a second example, if C is the collection of all open subsets of the real line, we can clearly obtain all subsets of F as intersection of an element of C and F.

The dichotomy in question is that, in fact, those two examples are typical in the following sense: either one can, for all n, find an n element set F and recover all its subsets as intersection with C (as in the second example); or for any n and any F in X of size n, the number of subsets obtained from F by intersecting with C is bounded by a polynomial function of n. So it is not possible to have intermediate behavior (subexponential growth which is not polynomial), and this is certainly surprising at first (at least for me).

This very nice fact is due to Vapnik-Chernovenkis and Shelah, independently (published in 1969 and 1971, respectively). What is quite remarkable is that the first authors were interested in basic probability theory (they found conditions for the “empirical” probability of an event in the standard Bernoulli model to converge uniformly to the mathematical probability over a collection of events, generalizing the weak law of large numbers), while Shelah was dealing with model-theoretic properties of various first-order theories (in particular, stability).

In fact, these references are given by L. van den Dries (Notes to Chapter 5 of “Tame topology and O-minimal structures”, which is where I’ve read about this, and which is available in the Google preview), but whereas it’s easy to find the result in the paper of Vapnik-Chernovenkis, I would be hard put to give a precise location in Shelah’s paper where he actually states this dichotomy! This is a striking illustratation both of the unity and divergence of mathematics…

The proof of the dichotomy, as one can maybe expect (given the information that it is true), is clever but fairly simple, and gives rather more precise information than what I stated. Let’s say that C is a rich uncle of a finite set F if any subset of F is the intersection of F with a subset in C. We must show that either C is a rich uncle for at least one finite subset of every order, or else C only represents relatively few subsets of any finite subset.

First, a lemma states that:

Given a finite set of size n and a collection D of subsets of F, which contains (strictly) more subsets than there are subsets of F of size up to (but strictly less than) some d, one can always find in F a subset E of size d such that D is a rich uncle of E.

Note that this is best possible, because if we take D to be those substes F of size up to (and excluding) d, it certainly can not be a rich uncle of a set of size d.

If we grant this lemma, the proof of the dichotomy proceeds as follows: assume we are not in the first case, so for some d, C is a rich uncle for no subset of order d. Let n>d be given (to get polynomial behavior, we can restrict to this case), and let F be a subset of order n. The lemma (applied with D the intersections of C with F), and the definition of d, imply by contraposition that the number of subsets of F which are obtained by intersection from C is less than the number of subsets of a set of order n which are of order d at most. But this is a polynomial function of n, of degre d.

As for the lemma, I leave the proof as an exercise (see page 80 in the book of van den Dries, which is also in the preview), with a hint: proceed by induction on n. (One is tempted, in view of the statement, to use the pigeon-hole principle to say that D must contain one subset at least of order d, but the proof by induction doesn’t use that).

Now I am going to try and think if I can find some other application of this fact…