As a number theorist interested in probability, I have accumulated my knowledge of that field (such as it is…) in a rather haphazard fashion, as is probably (pun intended) typical. The gaps in my understanding are wide and not really far between, and I can’t generally expect to take advantage of teaching a class to fill them (we have very good probabilists in Zürich), though I did teach introductory probability two years in Bordeaux. So it’s not so surprising that I stumbled this morning in my lecture on expanders when defining a Markov chain (which deserves some “tsk, tsk” from my ancestors, since my mathematical genealogy does trace back to Markov…)
More precisely, given a graph , say
-regular, I defined a random walk on
as a sequence
of random variables taking values in the vertex set
, and which satisfy the conditional probability identity
for all , and all vertices
, where
is the number of edges (unoriented, oeuf corse) between
and
.
But, as one of the CS people attending the lecture pointed out, this is wrong! The definition of a Markov chain requires that be able to condition further back in the past: for any choices of , one asks that
which corresponds to the intuition that the behavior at time be independent of the part trajectory of the walk, except of course for the actual value at time
.
What puzzled me no end was that I had failed to notice the problem, simply because this more general condition did not play any role in what I was doing, namely in proving the convergence to equilibrium of the random walk! The difference, which was clarified by my colleague M. Einsiedler, is that although the “wrong” definition allows you to compute uniquely the distribution of each step as a function of the initial distribution
, and of the transition probabilities
, one needs the actual Markov condition in order to compute the joint distribution of the whole process
, i.e., in order to express such probabilities as
as functions of the distribution of and the transition probabilities.
(My confusion arose partly from the fact that, up to this class, I exclusively used random walks on groups as Markov chains, defined using independent steps, and these are automatically Markovian; I’ve actually exploited the “strong” Markov property in a recent paper with F. Jouve and D. Zywina, but in that specialized context, the point above — I’m not sure if it deserves to be called “subtle!” — didn’t register…)
That must have been an unsettling experience indeed…
A funny thing, as you noticed, is that the difference between the two hypotheses is invisible when one looks at the distribution of any given position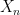 , and even when one looks at two successive positions
, and even when one looks at two successive positions 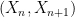 , but that it can become visible when one looks at *three* successive positions
, but that it can become visible when one looks at *three* successive positions 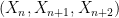 .
.
For a simple example of this, fix a positive parameter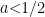 and consider two different processes on a discrete circle
and consider two different processes on a discrete circle  with
with  . The Markov version is the Markov chain on
. The Markov version is the Markov chain on 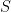 such that, when at
such that, when at  , one stays at
, one stays at  with probability
with probability 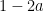 , one jumps at
, one jumps at 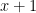 with probability
with probability  and one jumps at
and one jumps at 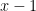 with probability
with probability  .
.
In the non Markov version, one first draws a sign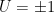 at random, with equal probabilities for
at random, with equal probabilities for  and for
and for  . The value of
. The value of 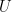 decides whether the process moves clockwise or anticlockwise. More precisely, when at
decides whether the process moves clockwise or anticlockwise. More precisely, when at  , one stays at
, one stays at  with probability
with probability 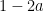 , and one jumps at
, and one jumps at  with probability
with probability 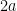 .
.
Finally, assume in both cases that the initial position is unfoirmly distributed on
is unfoirmly distributed on 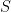 . Then, for every time
. Then, for every time  , one can check that in both cases
, one can check that in both cases 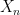 is uniformly distributed on
is uniformly distributed on 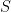 and
and 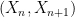 is uniformly distributed on the set of the
is uniformly distributed on the set of the  pairs
pairs 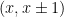 with
with  in
in 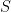 .
.
But the event![[X_n=X_{n+2}\ne X_{n+1}] [X_n=X_{n+2}\ne X_{n+1}]](https://s0.wp.com/latex.php?latex=%5BX_n%3DX_%7Bn%2B2%7D%5Cne+X_%7Bn%2B1%7D%5D&bg=ffffff&fg=000000&s=0) (aka *doing a U-turn*) has positive probability in the Markov case and zero probability in the non Markov case.
(aka *doing a U-turn*) has positive probability in the Markov case and zero probability in the non Markov case.