Analytic number theorists often work with multiple sums and integrals. In fact, sums are sometimes so congenial that the more there are, the merrier, and it may be quite a deep step to split a single sum into two. A famous examples is found, for instance, in Iwaniec’s celebrated bilinear form of the remainder term in the linear sieve, where one goes from something like
to an expression involving two variables (say n and m)
with
and more or less unknown (but essentially bounded) coefficients α and β. (For a very clear discussion of why this is of crucial importance in some important problems of analytic number theory, and why the second form is more useful than the first, see for instance the Section entitled “The remainder term” in this survey paper of J. Friedlander).
In this spirit of increasing sums unboundedly, here is the record-holder I’ve seen so far (if memory serves): it is equation (29) in a paper of M. Young on non-vanishing of central values of L-functions of elliptic curves. Here is a screenshot:
where one counts no less than 11 summation signs.
Does any reader have a better example at hand? Examples involving the composition of more than 11 derived functors are also welcome for this friendly competition.
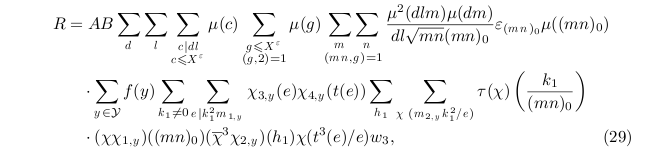
This is one contest I hope I don’t win!
I remember Katz giving a talk where an H^8_etale(X,F) came up “naturally”, although I don’t remember the details.
I’ve heard that Hendrik Lenstra once presented a commutative diagram connecting 76 different objects during a talk.