The Mertens formula

The Mertens formula is the name given to the asymptotic determination of the behavior of the partial products of the Euler product for ζ(s) at s=1, where the zeta function has a pole: precisely, it is the statement that

$\prod_{p\leq x}{\Bigl(1-\frac{1}{p}\Bigr)}\sim \frac{e^{-\gamma}}{\log x}$

as x tends to infinity (the product being of course restricted to primes), with γ being the Euler constant:

$\gamma=\quad \lim_{x\rightarrow +\infty}{\Bigl(\sum_{j\leq x}{\frac{1}{j}}-\log x\Bigr)}=0.57721566490153286060651209008240243104\ldots$

This formula has a special place in elementary prime number theory in that, although the asymptotic behavior is not so deep (at the level roughly of Chebychev-type estimates), and it is very easy to prove, from the Prime Number Theorem, in the form

$\prod_{p\leq x}{\Bigl(1-\frac{1}{p}\Bigr)}\sim \frac{e^{-c}}{\log x}$

for some constant c, the fact that this constant is none other than γ is not a purely formal consequence of the Prime Number Theorem. And if one looks at the standard treatments (e.g., in Hardy & Wright, and in Tenenbaum’s book, which follow more or less the same reasoning), it’s hard to come back with a clear explanation of why this is so, and what this constant may possibly mean.

I’ve been thinking about this the last few days because of something that looked very much like a serious problem in my joint work with A. Nikeghbali (which I’ve described earlier — the paper will be posted soon) on analogies between random matrices, zeta, and the Erdös-Kác theorem. This was pointed out to us by P. Bourgade: in the post above, I said

Well, one can clearly expect a finite-field version of the mod-Poisson convergence for ω(f), where f ranges over monic polynomials of degree d tending to infinity over a fixed finite field:
$\frac{1}{q^d}\quad\sum_{\deg(f)=d}{e^{iu(\omega(f)-1)}}\quad\sim_{d\rightarrow +\infty}\quad \exp((\log d)(e^{iu}-1))\gamma_q\Phi_1(u)\Phi_3(u),$
where there is an innocuous constant γ_q>0, the function Φ₁ is the same as before (i.e., it comes from random permutations), and
$\Phi_3(u)=\prod_{\pi}{(1-1/q^{\deg(\pi)})^{e^{iu}}(1+e^{iu}/(q^{\deg(\pi)}-1))},$
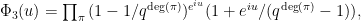
where the product runs over irreducible monic polynomials in A (so it is completely analogous to the Euler product for Φ₂…)

and although I didn’t write down the “innocuous” constant, its value, as we had it in our paper, was given by

$\log \gamma_q=\sum_{\pi}{\Bigl(\log(1-\frac{1}{q^{\deg(\pi)}})+\frac{1}{q^{\deg(\pi)}}\Bigr)}+\sum_{j\geq 1}{\Bigl(\frac{\Pi_q(j)}{q^j}-\frac{1}{j}\Bigr)}$

where the sum ranges over irreducible monic polynomials in F_q[T] and

$\Pi_q(j)=\sum_{\deg(\pi)=j}{1}$

is the number of such polynomials of degree j.

The problem with this, as Bourgade pointed out, is that if one takes u=0, then obviously everything that depends on u can be evaluated, and the purported formula becomes

$1=\gamma_q,$

and this doesn’t sound reasonable at all at first sight, in view of the expression we have for γ_q. In particular, because the origin of this constant is really the (or an) analogue of Mertens’s formula for F_q[T], namely

$\prod_{\deg(\pi)\leq d}{\Bigl(1-\frac{1}{q^{\deg(\pi)}}\Bigr)}\sim_{d\rightarrow +\infty} \gamma_q\exp\Bigl(-\sum_{1\leq j\leq d}{\frac{1}{j}}\Bigr)\sim \gamma_q\frac{e^{-\gamma}}{d},$

this sounded particularly implausible (to me at least) since it did not seem reasonable to expect that the very much simpler arithmetic of polynomials over a fixed finite field could lead so easily to the same highly transcendental-looking constant that occurs for the ordinary primes: recall that the analogue of the zeta function is the much simpler function

$\zeta_q(s)=\frac{1}{1-q^{1-s}}.$

So we looked for mistakes elsewhere, and this being the nature of preprints, we found a few minorish ones around this part of the proof, which however didn’t lead to any resolution of that problem.

And in fact, there is no problem: it is true that γ_q=1 for all q. It is psychologically amusing that I convinced myself of this not by searching Google for “Mertens function field” (which immediately gives suitable references), but by deciding to test numerically the behavior of the expressions

$\exp\Bigl(\sum_{1\leq j\leq d}{\frac{1}{j}}\Bigr)\times \prod_{\deg(\pi)\leq d}{\Bigl(1-\frac{1}{q^{\deg(\pi)}}\Bigr)}$

for various d and q: the convergence to 1 is unmistakable.

At that point I did look for references (it being even less likely to be new than the remark on the spectrum of multiplication operators). Possibly from “post-internet bias”, the earliest reference found is a paper of M. Rosen from 1999, in the J. Ramanujan Math. Soc., which unfortunately I have not been able to access. However, at least three other papers contain a proof (but I have only looked at two of them): this one by M. Car (2007), this one by P. Lebacque, and a possibly unpublished version by K. Conrad which is quoted by M. Car. Judging from the (short) Math Review, it seems that Rosen adapts the classical proof, and M. Car certainly does the same.

However, having these references is only a double-check: since our original argument was, in fact, correct, the remark of Bourgade amounts to saying that we have a (different) proof of the Mertens formula for polynomials over a finite field, in the form above:

$\prod_{\deg(\pi)\leq d}{\Bigl(1-\frac{1}{q^{\deg(\pi)}}\Bigr)}\sim_{d\rightarrow +\infty} \exp\Bigl(-\sum_{1\leq j\leq d}{\frac{1}{j}}\Bigr).$

And because of the way this is done, we understand much better where the constant comes from. In fact, there is really no constant: the right quantity to consider for product over irreducible polynomials of degree at most d is

$\exp\Bigl(-\sum_{j\leq d}{\frac{1}{j}}\Bigr),$

and for primes up to x, it is

$\exp\Bigl(\quad-\sum_{1\leq j\leq \log x}{\ \ \ \ \ \frac{1}{j}}\Bigr).$

And this factor is explained by the similar behavior of random permutations: it arises because the probability that a random permutation of n letters has no cycle of length at most d is approximately

$\exp\Bigl(\quad-\sum_{j\leq d}{\ \ \ \ \ \frac{1}{j}}\Bigr)$

when n gets large. (For d=1, this is the density of derangements, which is well known to be asymptotically 1/e).

In fact, this should have led us to understand immediately that our constant γ_q has to be 1, since this explanation of the way the Mertens formula looks is explained (by analogy with permutations, but without proof) in the survey of Granville which I had already mentioned in the earlier post (see the “Academic’s aside” on the bottom of page 5, and the discussion before). Our own proof is very much related: we relate polynomials with no small factors to permutations without short cycles, and use suitable equidistribution statements to get the same density.

Published by

Kowalski

One thought on “The Mertens formula”