After the free but snowy afternoon of Wednesday, and a nice conference dinner to gather new energy and strength, the conference started anew on Thursday morning. And here is what transpired that day… (I realize that those readers who only really want to know about one of the –excellent — short talks of Friday afternoon are now in a state of expectation such that even tomorrow’s relatively important event is being forgotten, but maybe this is a good thing really).
The first talk was given by M. Krishnapur and I unfortunately missed it because of teaching duties. However, reliable sources told me the talk was excellent, and he gave me a summary in the afternoon after the end of the day. It was probably the most “purely probabilistic” talk, and was devoted to ideas found in this paper of his concerning the singular values of certain random matrix-valued analytic functions, i.e., zeros of det F(z) where
where G_k are independent random matrices where each coefficients are themselve independent identically distributed gaussian variables. The main result is that those zeros in the unit disc form a determinantal process: this feature means that the probabilitity density for having zeros “very near” points
is of the form
for some kernel function K. This is extremely useful apparently for further study of the process, and I refer to the (excellently written) introduction and Appendix 9 of Krishnapur’s paper, since I am far from being an expert here.
Next came the talk of F. Mezzadri which was again particularly fascinating (at least for me). The motivating problem he discussed was to understand the distribution of the zeros of the derivative of the characteristic polynomials of random (Haar-distributed) unitary matrices. Those, because of the Gauss-Lucas theorem, all lie inside the unit disc, and the question is to understand the distribution of the number of zeros within an annulus with a well-chosen radius close to the unit circle — normalized so as to obtain a meaningful behavior as the size N of the matrices grows. Arithmetically, this can be expected to be related to the horizontal distribution of the real parts of zeros of ζ'(s) (it is known that, under the Riemann Hypothesis, all zeros of ζ'(s) are on the right of the critical line: this is the analogue then of the Gauss-Lucas theorem).
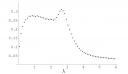
Now this might seem like just one more question among many others, but it becomes rather more like a taunt once you look at the experimental graph
(found on page 20 of the PDF file) for the relevant density. As Mezzadri mentioned, the behavior at 0 and at infinity are fairly regular and rigorously proved, but the “middle range” is not at all theoretically understood. Of course, one can’t help noticing the two bumps there (around 1 and 3 on the graph), and clearly all self-respecting mathematicians will want to know why they are there! (It is not clear in fact that the bumps will remain in the limit N goes to infinity, but even that would require an explanation; as seen on page 29, the experimental distribution of the real parts of zeros of the derivative of the Riemann zeta function seems remarkably close, though in the expected link between the two, the heights of zeros investigated in this second graph only corresponds to matrices of size 42 instead of 100 in the first graph).
Mezzadri then discussed the current approach he is using, with Man Yue Mo, to try to understand this middle range. This involves the Riemann-Hilbert approach and Töplitz determinants, and I will not try to say more.
The last talk of the morning was by C. Delaunay. This described his recent work with F.X Roblot (Lyon) concerning the algorithmic, heuristic (and rigorous when possible) study of those quadratic twists of a given elliptic curve E/Q which have odd rank/odd sign of the functional equation, and in particular that of the twists of rank 1 (which are expected to dominate among all those odd-rank twists). The difficulties are familiar from the study of number fields, especially real quadratic fields: assuming the Birch and Swinnerton-Dyer conjecture (for which much more is known in the rank 1 case than in the general case, from the Gross-Zagier formula and the modularity of elliptic curves over Q), the resulting formula for the central derivative of the L-function
for a rank 1 curve involves a product of the order of the Tate-Shafarevich group (a mysterious object, if ever there was one…) and of the “regulator” which measures the size of the numerator and denominator of a generator of the Mordell-Weil group. Delaunay and Roblot have managed to suggest conjectures for moments of the regulators of odd twists of the type
(sum over negative discriminants such that the rank of the twist is 1) when
(why this condition? because one can expect — from Cohen-Lenstra type heuristics — that the k-th moment of the order of the Tate-Shafarevich group will have a well-defined limit here). Quite significantly, they have also succeeded in accumulating a very large amount of data that gives strong hints that this is correct. For this purpose, they produce an algorithm that computes the three invariants
in less time than typical “naive” approaches would require to compute only the first one! (This is based on the Heegner point approach and modular parameterizations, with many tricks in between).
And then came a well-deserved lunch break once more (during which, to the dismay of those readers who are waiting for an account of his announced talk on rational zeros of ternary quadratic forms, H. Iwaniec was convinced by the random fall of a biased coin to switch his topic to a presentation of his recent work with Conrey and Soundararajan on the 6th-moment of special values of Dirichlet L-functions, where the mythical number 42 first appears in a rigorous manner…).
The afternoon was devoted to two related talks by G. Ricotta and E. Royer, who presented their recent works on the 1-level density of low-lying zeros of symmetric power L-functions of classical (holomorphic) modular forms. G. Ricotta first presented the background material needed, and stated the main result, where the main feature is that a lower order term is found for this 1-level density function. This behavior is expected and analogue predictions for the Riemann zeta functions were discussed by J. Keating during his talk at the conference, but not many theoretical results are known yet in this direction, so the work of Ricotta and Royer is a very useful contribution. From the number theory point of view, note that the main novelty in this type of lower-order terms is that they definitely involve number-theoretic features, related to the distribution of primes, whereas the main term is “universal” and can be interpreted purely in terms of Random Matrices.
The second part of the talk, by E. Royer, described some features of the arguments used in the proof. His emphasis was on the fact that computations which could easily look as if they were inextricable in this setting, were in fact fairly simple — and in fact elegant — when the right point of view was taken: namely, the question is to understand various polynomial averages of local Hecke-eigenvalues
Such expressions are, in some sense, equivalent: each can be transformed into the other, but if one is not careful, this leads to a lot of combinatorial identities which can seem pretty obscure, when in fact the crucial insight is to use systematically the basis of the space of polynomials given by the Chebychev polynomials Xn such that
(for unramified primes). This is often obvious and barely worth stating for algebraists, but not at all for analytic number theorists who have not learned early enough of the representation theory of SL(2). Royer mentioned a few combinatorial identities that can be quickly derived from such considerations in a much cleaner way than the direct “binomial-coefficient” approach that is also possible (see the Appendix to the paper).