Here is an amusing thing I hadn’t properly realized until recently: depending on the definition, the Cayley graph of with respect to the symmetric generating set
can be either a single arrow joining two vertices
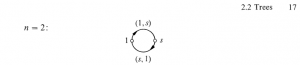
or a cycle of length 2:
The first case occurs when one is not careful, taking as edge set of the set
(as was probably to be expected, my notes on expander graphs use this naïve definition…)
The second case occurs (at least) when one is Serre, as can be checked from the definition in “Trees”, and the resulting illustration:
(in a French printing of that book which I have seen, Serre specifically warns that the two edges are not the same).
The questions are, which is the “right” definition, if any? and should this matter? To a large extent, the answer to the second is (fortunately) “not really”, though the same issue arises for any Cayley graph where some generator is an involution.
Either choice has some potentially annoying features:
(1) The canonical choice (Serre’s) has the effect that any Cayley graph of a group with respect to a generating set containing an involution has multiple edges; for instance, the following picture taken from P. de la Harpe’s “Topics in geometric group theory”
is supposed to be the Cayley graph of with respect to a generating set for which it is a free product of cyclic groups of order 2 and 3 (generated by
and
, respectively), but is wrong with the canonical definition. (To be fair, de la Harpe mentions the issue, and says that he uses the naïve definition because that is not a problem for his purposes.)
(2) In the canonical choice, the formula
for the Markov averaging operator is usually wrong. (E.g., for the example of above.) In particular, the spectrum of the Laplace operator is not the same depending on which definition is used…
(3) Similarly, the Cayley graph is not always
-regular.
(4) However, in the non-canonical choice, it follows that a Cayley graph of a finite group may have infinite girth (being a tree, as in the example of …) Correspondingly, the interpretation of the girth of a Cayley graph as the smallest length of a non-trivial relation in the generators may fail…
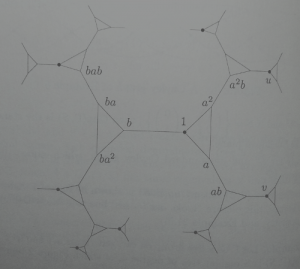
At the moment, as I said, I use the naïve definition in my notes (most books I’ve seen which bother to define the Cayley graph in a formally precise way seem to do the same, though the definition is often sufficiently fuzzy that it doesn’t take much effort to accommodate both possibilities…) But I claim somewhere that the Cayley graph of (with respect to
) is a cycle of length
, which is then wrong for
.
I haven’t quite decided how I will change the text, since I tend to like the formula for the Markov averaging operator. Maybe, like de la Harpe, I will just mention both possibilities and use the naïve one. Certainly, as far as expander graphs are concerned, this has no consequence on the property of being or not an expander for a sequence of Cayley graphs (of bounded valency).
The illustration you show from Serre is for a directed 2-cycle, which is different from the undirected 2-cycle you show before it. Before you decide about 2-cycle vs single edge, you need to make a more fundamental decision about directed vs undirected.
When defining undirected Cayley graphs, I prefer the definition that creates a single undirected edge for an involution, because it allows for many symmetric odd-degree graphs to be Cayley graphs, which is useful when dealing with the same graphs for other reasons and wanting to impose a group-theoretic structure on them.
You’re right about the picture! I pasted it too quickly from the English translation of “Arbres, amalgames and ”. I will check tomorrow the French version, where I remember seeing the construction of the un-oriented Cayley graph with the two edges (the definition starts with an oriented graph, and then passes to an unoriented one, and — as stated by de la Harpe –, the latter has no multiple edges if and only if there is no involution in the generating set.)
”. I will check tomorrow the French version, where I remember seeing the construction of the un-oriented Cayley graph with the two edges (the definition starts with an oriented graph, and then passes to an unoriented one, and — as stated by de la Harpe –, the latter has no multiple edges if and only if there is no involution in the generating set.)
I second David as to directed/undirected Cayley diagrams. I was led to the same conclusion by the following argument. (Below Cayley graph is Cayley diagram with labels)
For technical reasons, it’s good to have Cayley diagrams also for sequences (so that we might have couple of arrows with the same label going from one vertex to another). For example when one considers elements of the integral group ring whose coefficients are positive, but not always 0/1.
When is a sequence of generators symmetric? If every group element appears exactly the same number of times as its inverse. We know how to define an oriented Cayley graph wrt to a sequence. And if a sequence is symmetric, we define the unoriented Cayley graph by taking a representative from each “pair”.
The reason for “pair” being in inverted commas are of course elements of order 2, because precisely they don’t have to be paired in symmetric generating sequences.
sorry, the comment in brackets should be (Below Cayley diagram is Cayley graph with edge labels)
Multiple egdes should not be the problem. Anyway the quotient of the Cayley graph by the group is a bouquet which has multiple… loops.
I suppose one should blame for “noncanonical definition” lousy geometric group theorists for whom the Cayley graph is just a one-skeleton of the universal space (contractible scace with free action). They immediately glue relations (and so on) to the graph (in order to kill homotopy). Therefore the two directed edges become the boundary of the unique disc, a thick edge.
There is one situation when “noncanonical” Cayley graph turns to be useful. This is when the group is generated just by involutions.
One way to define Coxeter groups is to say that those are exactly groups generated by involutions with the property that the set of fixpoints of every generator disconnects the “noncanonical” Cayley graph.
As a topologist, I think the right definition is Serre’s, as it allows you to avoid talking about symmetric generating sets and just take the Cayley graph to be the 1-skeleton of the universal cover of a presentation 2-complex (the complex with 1-skeleton a rose on your generating set and 2-cells for the relations).