I have mentioned one type of fractal already, but nature’s favorite (or at least, my own favorite…) is probably the curve formed by the path of a standard Brownian Motion, which is mathematically thought of as being a “random” continuous function
and is visualized by the graph of this function. One can find online plenty of pictures of “typical” paths, which are immediately noticeable by virtue of being very rough: indeed, it is a theorem of Paley, Wiener and Zygmund that, almost surely, the function
is nowhere differentiable, hence violent oscillations must exist arbitrarily closely to every point of the graph.
Hence the typical pictures of simulated Brownian motion are not as striking or beautiful as those of approximations of other fractal objects can be. This seems to be a shame, and things don’t have to be this way: since we can only draw approximations, the problem is partly that Brownian motion is often approximated by rescaled random walks with smaller and smaller steps with affine interpolation of the discrete steps of the walk, which creates the spiky look at each change of direction.
But here’s my own version:
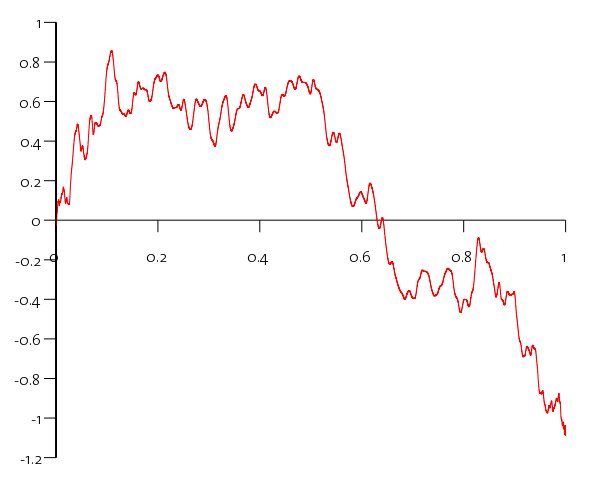
Isn’t it much nicer? Or, at least, more “readable”?
The theoretical backround is the theory of Bernstein polynomials (S. Bernstein, not J. Bernstein, who also has his own polynomials). They were used by S. Bernstein to provide a nice constructive proof of the Weierstrass approximation theorem: for any continuous function
the polynomials
converge uniformly to f as n goes to infinity. Since those are polynomials, they are very smooth approximations to an arbitrary continuous function. And if one applies this to a path of the Brownian motion, using the known distribution of the random variable B(i/n) (namely, a standard centered gaussian with variance i/n), one gets nice polynomial approximations of Brownian motion! The one above has degree 40000, and it should be said that trying to compute it from the formula doesn’t work (binomial coefficients (40000/i) are not so easy to compute when i is reasonably big…): what is used instead is the probabilistic interpretation of
as the probability that a binomial distribution with parameters x and n (i.e., the sum of n Bernoulli random variables with probability of being 1 equal to x) takes value i; this is approximated nicely by packages such as GSL. On the other hand, it takes much longer to output a graph like the one above, compared with a random walk with similar complexity (interpreted, roughly speaking, as how complicated the graph looks like — how many changes of direction, for instance).
All of this is described in the first part of my paper on Bernstein polynomials and Brownian motion (note that the last section of this, which tries to study zeros of random Bernstein polynomials, contains a serious mistake…); in particular it is shown that, indeed, those converge (in law) to Brownian motion, and in fact can be used to give an alternative proof of its mathematical existence.
Thanks for your Bernstein paper and its wonderful bibliography.
Einstein’s title
“Uber die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen”
vividly shows( twice!) the pecularity of the by the possibility of having phrases functioning as adjectives enriched German language.